User:R.o.b.stiemsma@student.tue.nl/SLAMwriteup

FastSLAM2

In order to describe FastSLAM2, as well as the choice to use it, we will use deepening steps from the overall problem of SLAM, through the generic strategies to solve it, down into the algorithm itself.

The SLAM Problem

To solve the SLAM problem is to answer the age-old question

What came first, the chicken or the egg?

In less symbolic language, let's put it this way: during operation of the robot, in almost every timestep k ∈ ℕ, we attempt to answer the question 'Where are we?`, which implicitly contains two much more concrete questions;

What is my position, relative to my surroundings?

What are my surroundings and their meaning or position relative to me?

Without any mathematics involved, one can already start to see an emerging intrinsic relationship between the localisation problem and the mapping problem.

Certainty cannot be achieved during timestep k, and as such, the art is to get as much certainty as is possible without exceeding a bearable workload (as to find ourselves too computationally burdened to be ready for the next timestep, k+1. There are many ways to cope with this problem, from the simplistic `not dealing with it at all`, using a Zero-Order Hold (ZOH), or a ZOH with inclusion of the proposed movement and positions from the current timestep, all the way to the rather absolute, offline `GraphSLAM` method, which saves countless measurement points, and tries to optimize the sense these points make relative to each other (or: attempts to minimize the magnitude of discrepancy between measure points).

Our problem is marked by being online (PICO needs to know what's going on while it's happening) in a rigid environment, under uncertain starting conditions, with noisy motion and noisy measurements. PICO additionally has to deal with random, dynamic elements, which one could attempt to deal with in the SLAM module of a program, but we won't, simply so we can keep using a rigid world assumption. Instead, the workload for coping with dynamic elements will be on feature recognition, which will have to make the judgment call to name a random element static (and add it to the map of rigid elements) or dynamic.

In the world of online SLAM methods, we will very quickly find ourself submerged in the world of world features considered through Extended Kalman filters (EKFs), and since we have noise (or: a constant threat to localization certainty), as well as an uncertain starting position, we will also find ourselves looking to use a particle filter as to not find ourselves locked into a single wrong hypothesis.

This brings us to the next section, where we will explain what the inner workings of an EKF particle filter are.

Simultaneous Localization and Mapping using Particle Filters

In this section, we will expand on the basis given by the course lectures. Most additional knowledge here is derived from the (freely available) lectures on SLAM by Cyrill Stachniss, a full-time professor at the university of Bonn.

The Particle Filter Side

Let us consider first the particle filter side of our fledgling concept of SLAM. Each particle within the cloud of n particles represents a hypothesis, containing within itself a presumed location (x,y) of the platform - PICO - and its assumptions about the surroundings - the EKF part of the problem. With each update, these hypotheses are somehow updated under assumptions about the predicted motion since the last timestep and under interpretation of the measurements received in the current timestep. The idea is that if the problem is observable and noise is adequately respected, the cloud of hypotheses will continuously converge on a correct solution, giving a supposedly ever-sharpening fuzzy localization that can be adequately used as a substitute for a true notion of the platform's pose (location and rotation) in the world.

The crux of a particle filter solution is to somehow weight assumptions with measurements. To keep things formal, let us steal a little part of the EKF side of the problem, and already introduce the concepts of a prior (the assumed position) and posterior evaluation (the expected position based on measurements). This, formally, gives us the following primary mechanic to work our particle filter with:

Armed with a definition for the weight (or 'belief') we give a certain hypothesis, we can talk about the workings of our particle filter. After every timestep, every particle - and thus every hypothesis - has been given a weight; these weights have meaning relative to one another, and for the sake of keeping the risk of binary overflow errors to an minimum, these are linearly normalized somehow relative to some measure - e.g. the sum weight or the maximum weight.

We now steal a page from the concepts constituting machine learning; we cull hypotheses that are too weak, and let the likely hypotheses dominate the cloud. That is: some particle's respective weights, after normalization, are weaker than some minimum parameter, and so these hypotheses are destroyed. After this, we somehow decide whether our hypothesis population is underpopulated, and repopulate it with n_new new particles based on the pool of hypotheses we currently have during a resampling process. This resampling process is best described as spinning a wheel, where the portions allocated for particular particles on this wheel are scaled depending on their weights.

Literature suggests that low-variance resampling is the way to go here, which is an algorithm that is often instead called 'roulette wheel resampling'. The idea is that normal spin-the-wheel-with-every-pick resampling has a (completely unnecessary) chance to arbitrarily favor a particular group of hypotheses by repeatedly picking their members as resampling candidates. Roulette wheel resampling, instead spins the wheel once, and then jumps around the wheel n_new times, with jumps scaled by the total weight of all particles, divided by n_new.

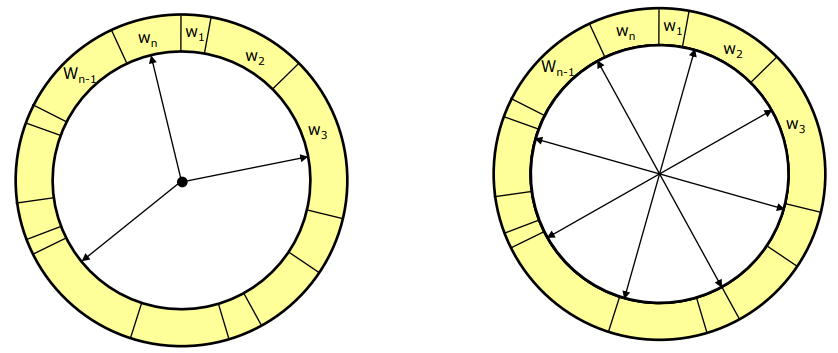
The above picture, from Stachniss' slides on probabilistic robotics, are a clear illustration of the normal pick-every-sample algorithm (left) and the roulette wheel approach (right). Note that, additionally, the simple approach has algorithmic time complexity O(n log(n)), as every sampling also needs to be looked up by index in the particle list, whereas the roulette wheel approach does lookup intrinsically as part of generating the 'spokes' of the wheel, and hence has algorithmic complexity O(n).

This concludes the particle filter side of our understanding of SLAM. In one pseudocode block, let us summarize the core concepts before we dive into the ugly side that is Gaussian predicates:

Cloud particleFilter(Cloud particles, PredictedMotion u, Observation z) { 
   for each particle in particles :
      particle = updateParticle(particle, u, z);   
      // To be defined in the EKF side of things. 
      // This step already updates the weights, but let's make it explicit.
      
      particle.w = updateWeight(particle, z); 
      // Evaluate assumptions based on observations.
   
   particles = normalizeWeights(particles);
   particles = cullWeakHypotheses(particles);
   particles = lowVarianceResample(particles);
 
return particles;
}

Given that we have some functional way to predict our behaviour and rate a hypothesis, and have made adequate decisions in defining our prior and posterior weight factors, we now have a particle filter that will continuously converge to an optimal hypothesis, without locking itself into a particular belief. In other words, we have described a learning algorithm that looks to minimize the localization error, but won't decide on a certain group of hypotheses until it gets evidence that sways it one way or another.

But we do not have the necessary mathematics in place yet, so... let's get that over with!

The EKF Side

This part leans heavily on the aforementioned lectures, and the research papers 'FastSLAM' and 'FastSLAM2.0' by Montemerlo, Thrun, Koller and Wegbreit.

For the mathematically intensive part of this problem, we will be dealing with probabilistic distributions and laws, such as p(s(k+1) | u(k+1), s(k)). This reads as 'the probability that we will see a certain pose s(k+1) at time k+1, given that we saw s(k) at time k while we've been told we moved with a vector u(k+1) this timestep.' To be precise, this particular distribution is already important enough to be denoted as an equation!

What we have just described is known as the probabilistic law that describes a motion model. To be more precise, assuming that u represents a shift in pose (rather than a vector of velocities), and both state vectors s represent robot poses (x, y, θ), and no outside influence, the average position of the robot will be s(k+1) = s(k) + Au(k+1).

As we have already discussed the particle filter side of things, this is also where we need to introduce the concept that our position shifts u(k) are noisy. In order to make our probability distribution truly a distribution, the idea is to have each particle updated both strictly with u(k), and with a random amount of process noise Q.

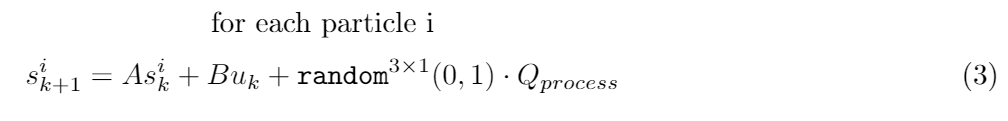
Where random generates a vector of 3 elements given random values according to the normal (float) distribution with mean 0 and st.deviation 1. Note that Qprocess is a representation of the noise in PICO's odometry, and hence a correct value will have to be measured, obtained from simulation settings (as a substitute to experimentation), or approached through tuning. As it is a compounding problem to try and dynamically calibrate noise covariance, this is out of consideration due to complexity alone - it would be like bringing another two smaller SLAM problems into the original SLAM problem.

The result of implementing (3) is that our particle filter - without any further logic - is an n-sampled representation of the motion law (1). Each timestep has the particles of our cloud spread out further, while adhering to the dynamics of u with each timestep. In other words, (3) implemented into a particle filter is an answer - but not a good answer - to the question `Where is my position, relative to my surroundings`.

Now we consider the other probabilistic law in SLAM, which just so happens to answer the other question posed at the start of this section;

Where we need to quickly introduce the concept of a landmark or feature. Within the confines of this project, it suffices to say 'corners', but in a more general sense: a landmark or a feature is something that the robot's sensors and feature recognition software can spot. Ideally, this is something that a robot can reliably and somewhat precisely pick out from its surroundings, but that is not formally part of the definition.

The law in (4) is known as the measurement model in literature. It talks about the probability that we make an observation z at time t, given that the robot has pose s(t), lives in the world w (which is a list of landmarks/features the robot can see), and that it has had some correspondence h(t) (which is an identifier for a certain landmark that is suggested to have been seen by the observation z). With other words, it is an answer to the question `I think I saw this. Should I see this?`, which is directly related to `what are my surroundings, and what are they relative to me?` when we apply it to more than a single observation. We're almost there!

Note that we have not introduced any notion of persistent landmarks; the set w can theoretically expand infinitely. The reason that this matters will become apparent shortly, when we combine the two probabilistic laws (2), (4) into a probabilistic definition of our SLAM problem:

Note that we now have superscripts t; this notation means 'from time t0 up to time t'. In normal English, (5) poses the question `How likely is it that I am here, and the world is what I think it is, given my prior observations, given the motion I've undertaken, and given the landmarks I've spotted?`. In even more normal English, this reduces to `Given that I've seen these things, am I right to think I am here?`.

If you'll remember the concept of weight from the particle filter side of things, this is the notion used to weight a certain observation. This probabilistic law is sufficient to set up an algorithm to localize a robot in a world with a limited amount of potential features, but as the process involves at least one inverse, and this inverse is currently tied to the size of the set w, this is very easily going to become computationally infeasible. This is where we move on to the fastSLAM part, where we will finally fill in the actual methods to turn probabilistic law into quantifiable outcomes.

FastSLAM and FastSLAM2

As a small recap, we have introduced the concept of a particle filter serving as a cloud of hypotheses, or guesses, to the robot's position, and the idea of probabilistic distributions that we can use to evaluate the feasibility of a certain measurement given a certain hypothesis and history.

The core idea that makes FastSLAM so powerful is its exploitation of the given fact that landmarks are static. This is best put in the following observation:

If we know the path of the robot, landmark positions can be estimated with respect to the robot, independently from one another.

This takes the form of another probabilistic law:

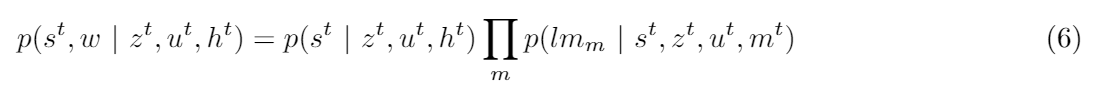
Where lm represents a particular landmark in the world set w, and mᵗ is the weight factor history of a certain landmark. In other words, we've here refactored the problem (5) into two much (computationally) lighter subproblems; that of the likelihood that the robot has a certain pose, and that of the compounded set of likelihoods that a certain landmark is seen the way it has been seen, if it has been seen, at a given time.

The reason that this matters is that the processes of updating and evaluating the measurement model involve inversions of covariance matrices with a size equivalent to the world set, plus the 'moving landmark' that is the robot itself. Inversions are an O(n³) operation.

In (5), the world set is the combined set of all landmarks, which in the hospital challenge by default were already in the order of 100 points; 100³ operations, every single iteration, for every particle and every correspondence, is a gigantic workload. In (6), however, the world set(s) is (are) much smaller; it is the local world of the considered landmark, which can be described through a mean position and, with PICO included into the equation, a 2x2 covariance matrix. 100 times 2³ is much, much smaller than 100³.

This allows us to formulate our particle filter as a system of n particles with m small internal models, one for each landmark in the global map. Each internal landmark model lm is stored with global coordinates, but a local origin; it describes a mean distance in (x, y) to the particle in question, with a covariance H describing how certain that mean is. This is compounded with a measurement covariance R that is used to account for measurement uncertainty.

This brings us to the basic operation of the FastSLAM algorithm, in pseudocode:

void FastSLAM(Cloud cloud, PredictedMotion u, ObservationSet zt){
   for each particle in cloud {
      // Predict
      particle.updatePose(u); // as per (3)
    
      // Observe
      for each z in zt {
         if(particle.lm[z.id].known)
            particle.updateLandmark(z);
            particle.w *= getWeight(z);
         } else {
            particle.lm[z.id] = particle.newLandmark(z);
         }
      }
   }
   
   // Adapt
   cloud = cullHypotheses(cloud);
   cloud = resample(cloud);
}

Where we implicitly also added an intuitive boolean evaluation of whether the robot has yet encountered a certain landmark. We have, however, yet to define the behaviour of making, updating, and evaluating landmarks. Given that an observation z is an LRF-measured landmark, represented as the tuple LRFLandmark(int id, float r, double th), we will first tackle the easiest of those to-be-uncovered elements in makeLandmark. Note that a particle contains its pose as a vector p = (x, y, θ), and that a landmark is represented as the tuple Landmark(int id, bool known, float x, float y, Matrix2f H, where known is set to false at initialization, and true forever after makeLandmark(), and a Matrix2f is a 2x2 matrix of floats (from the Eigen3 library).

Landmark Particle::makeLandmark(LRFLandmark z) {
   Vector2f pol2car_g = [cos(z.th + p[2]); sin(z.th + p[2])] // p[2] = robot angle
   Vector2f d         = z.r * pol2car_g;

   Matrix2f jacobian  = [
      d[0]/z.r,       d[1]/z.r;
      -d[1]/(z.r^2),  d[0]/(z.r^2)];
   Matrix2f invJ      = jacobian.inverse();

   Landmark lhs; 
   lhs.id    = z.id;
   lhs.mean  = p[0:1] + d;
   lhs.H     = invJ * R * invJ^T;
   lhs.known = true;
   // update the weight element of the Particle structure.
   weight    *= default_weight; // Set to 1 by default.

   return lhs;
}

Note that this pseudocode used a more matlab-esque notation for matrix and vector formatting than C++ uses. For further uses of the jacobian of a vector d and a range r, we will instead make use of Matrix2f getJacobian(Vector2f d, float r).

This leaves us to talk about updating a landmark. The covariance of a location measured by a certain PICO-measurement has been given as a quadratic function of the inverse of a measurement's Jacobian, and the generic uncertainty of the sensors doing the measuring. Speaking in normal English, this is an implementation of setting up operation of term right of the product-sum of equation (6). It is not possible to adequately weight an observation of sample size 1, and as such it isn't an implementation of the actual term. In fact, the line weight *= default_weight; is the real implementation! Don't worry, it'll get more complicated very quickly.

As described two snippets ago, an observation that isn't novel to the particle's knowledge will lead to an update. The idea here is to still start with the same principles in working with an introduced observation; the same local Cartesian distance vector is needed, the Jacobian is still needed, and the inverse of that Jacobian is still needed. However, the exact same operations are again applied to the particle's current knowledge of the considered landmark. That is, the relevant local polar coordinates, Cartesian coordinates, and measurement Jacobian are accumulated where the data wasn't already stored.

Now, the difficult part for the landmark update is constructing the Kalman gain part of an Extended Kalman Filter. The first step is to compute the same covariance as would have been computed to make a new landmark made fuzzy by the measurement noise. The Kalman filter used for the update is calculated as in equation (7)

Where the elements are landmark's current covariance H(t-1), the transpose of the Jacobian of the current observation, J(t) and the would-be covariance of the current observation H~(t).

Updating the landmark hypotheses are then functions of the computed Kalman filter and some measure of the change proposed by the established hypotheses and the proposition of the current measurement. These equations are given below in equation (8).

Now we are left with the dirty work that has been done over and over in established SLAM literature: weighting. The idea, as established in (1), in the part on particle filters, is to compute a prior and a posterior, and defining the weight as the prior divided by the posterior. The idea established in the lectures of Stachniss and the research papers of Thrun et al. is to describe the the weighting as finding how much probable correlation there is between measurement and hypothesis. The new information, or the target distribution, is a function of the covariance and Jacobian belonging to the current measurement, while the old information, or proposal, is a function of the current hypothesis' covariance and Jacobian. This uses a constituent matrix S(t), defined as

Which factors into the weighting as below

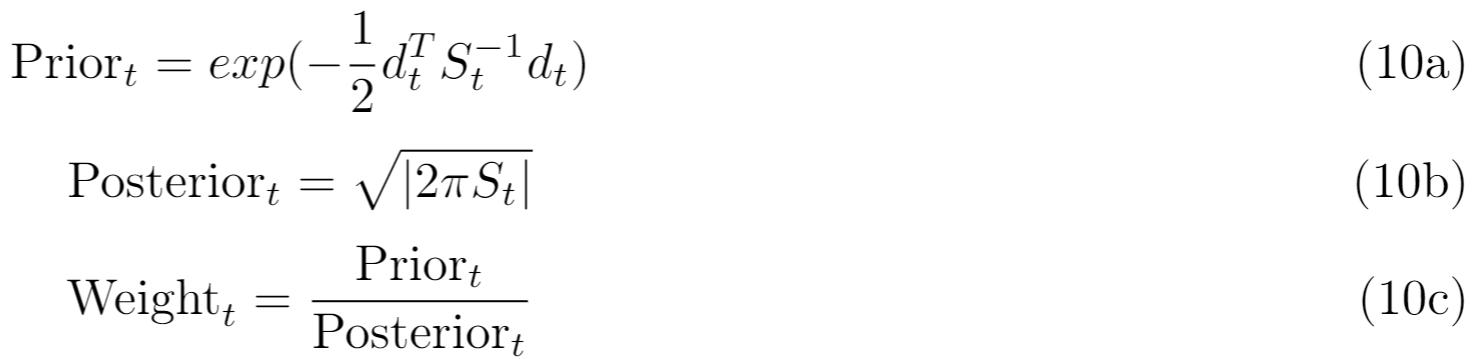
Given that d(t) is the distance between the current average position and position proposed by the current observation.