User:R.o.b.stiemsma@student.tue.nl/SLAMwriteup

FastSLAM2

In order to describe FastSLAM2, as well as the choice to use it, we will use deepening steps from the overall problem of SLAM, through the generic strategies to solve it, down into the algorithm itself.

The SLAM Problem

To solve the SLAM problem is to answer the age-old question

What came first, the chicken or the egg?

In less symbolic language, let's put it this way: during operation of the robot, in almost every timestep k ∈ ℕ, we attempt to answer the question 'Where are we?`, which implicitly contains two much more concrete questions;

What is my position, relative to my surroundings?

What are my surroundings and their meaning or position relative to me?

Without any mathematics involved, one can already start to see an emerging intrinsic relationship between the localisation problem and the mapping problem.

Certainty cannot be achieved during timestep k, and as such, the art is to get as much certainty as is possible without exceeding a bearable workload (as to find ourselves too computationally burdened to be ready for the next timestep, k+1. There are many ways to cope with this problem, from the simplistic `not dealing with it at all`, using a Zero-Order Hold (ZOH), or a ZOH with inclusion of the proposed movement and positions from the current timestep, all the way to the rather absolute, offline `GraphSLAM` method, which saves countless measurement points, and tries to optimize the sense these points make relative to each other (or: attempts to minimize the magnitude of discrepancy between measure points).

Our problem is marked by being online (PICO needs to know what's going on while it's happening) in a rigid environment, under uncertain starting conditions, with noisy motion and noisy measurements. PICO additionally has to deal with random, dynamic elements, which one could attempt to deal with in the SLAM module of a program, but we won't, simply so we can keep using a rigid world assumption. Instead, the workload for coping with dynamic elements will be on feature recognition, which will have to make the judgment call to name a random element static (and add it to the map of rigid elements) or dynamic.

In the world of online SLAM methods, we will very quickly find ourself submerged in the world of world features considered through Extended Kalman filters (EKFs), and since we have noise (or: a constant threat to localization certainty), as well as an uncertain starting position, we will also find ourselves looking to use a particle filter as to not find ourselves locked into a single wrong hypothesis.

This brings us to the next section, where we will explain what the inner workings of an EKF particle filter are.

Simultaneous Localization and Mapping using Particle Filters

In this section, we will expand on the basis given by the course lectures. Most additional knowledge here is derived from the (freely available) lectures on SLAM by Cyrill Stachniss, a full-time professor at the university of Bonn.

The Particle Filter Side

Let us consider first the particle filter side of our fledgling concept of SLAM. Each particle within the cloud of n particles represents a hypothesis, containing within itself a presumed location (x,y) of the platform - PICO - and its assumptions about the surroundings - the EKF part of the problem. With each update, these hypotheses are somehow updated under assumptions about the predicted motion since the last timestep and under interpretation of the measurements received in the current timestep. The idea is that if the problem is observable and noise is adequately respected, the cloud of hypotheses will continuously converge on a correct solution, giving a supposedly ever-sharpening fuzzy localization that can be adequately used as a substitute for a true notion of the platform's pose (location and rotation) in the world.

The crux of a particle filter solution is to somehow weight assumptions with measurements. To keep things formal, let us steal a little part of the EKF side of the problem, and already introduce the concepts of a prior (the assumed position) and posterior evaluation (the expected position based on measurements). This, formally, gives us the following primary mechanic to work our particle filter with:

Armed with a definition for the weight (or 'belief') we give a certain hypothesis, we can talk about the workings of our particle filter. After every timestep, every particle - and thus every hypothesis - has been given a weight; these weights have meaning relative to one another, and for the sake of keeping the risk of binary overflow errors to an minimum, these are linearly normalized somehow relative to some measure - e.g. the sum weight or the maximum weight.

We now steal a page from the concepts constituting machine learning; we cull hypotheses that are too weak, and let the likely hypotheses dominate the cloud. That is: some particle's respective weights, after normalization, are weaker than some minimum parameter, and so these hypotheses are destroyed. After this, we somehow decide whether our hypothesis population is underpopulated, and repopulate it with n_new new particles based on the pool of hypotheses we currently have during a resampling process. This resampling process is best described as spinning a wheel, where the portions allocated for particular particles on this wheel are scaled depending on their weights.

Literature suggests that low-variance resampling is the way to go here, which is an algorithm that is often instead called 'roulette wheel resampling'. The idea is that normal spin-the-wheel-with-every-pick resampling has a (completely unnecessary) chance to arbitrarily favor a particular group of hypotheses by repeatedly picking their members as resampling candidates. Roulette wheel resampling, instead spins the wheel once, and then jumps around the wheel n_new times, with jumps scaled by the total weight of all particles, divided by n_new.

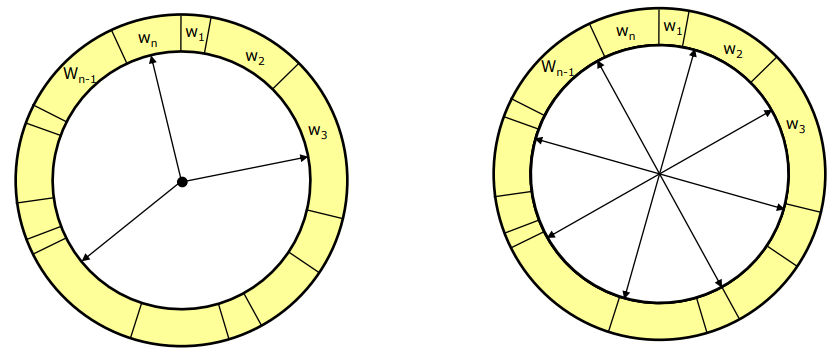
The above picture, from Stachniss' slides on probabilistic robotics, are a clear illustration of the normal pick-every-sample algorithm (left) and the roulette wheel approach (right). Note that, additionally, the simple approach has algorithmic time complexity O(n log(n)), as every sampling also needs to be looked up by index in the particle list, whereas the roulette wheel approach does lookup intrinsically as part of generating the 'spokes' of the wheel, and hence has algorithmic complexity O(n).

This concludes the particle filter side of our understanding of SLAM. In one pseudocode block, let us summarize the core concepts before we dive into the ugly side that is Gaussian predicates:

Cloud particleFilter(Cloud particles, PredictedMotion u, Observation z) { 
   for each particle in particles :
      particle = updateParticle(particle, u, z);   
      // To be defined in the EKF side of things. 
      // This step already updates the weights, but let's make it explicit.
      
      particle.w = updateWeight(particle, z); 
      // Evaluate assumptions based on observations.
   
   particles = normalizeWeights(particles);
   particles = cullWeakHypotheses(particles);
   particles = lowVarianceResample(particles);
 
return particles;
}

Given that we have some functional way to predict our behaviour and rate a hypothesis, and have made adequate decisions in defining our prior and posterior weight factors, we now have a particle filter that will continuously converge to an optimal hypothesis, without locking itself into a particular belief. In other words, we have described a learning algorithm that looks to minimize the localization error, but won't decide on a certain group of hypotheses until it gets evidence that sways it one way or another.

But we do not have the necessary mathematics in place yet, so... let's get that over with!

The EKF Side

This part leans heavily on the aforementioned lectures, and the research paper 'FastSLAM' by Montemerlo, Thrun, Koller and Wegbreit.

For the mathematically intensive part of this problem, we will be dealing with probabilistic distributions and laws, such as p(s(k+1) | u(k+1), s(k)). This reads as 'the probability that we will see a certain pose s(k+1) at time k+1, given that we saw s(k) at time k while we've been told we moved with a vector u(k+1) this timestep.' To be precise, this particular distribution is already important enough to be denoted as an equation!

What we have just described is known as the probabilistic law that describes a motion model. To be more precise, assuming that u represents a shift in pose (rather than a vector of velocities), and both state vectors s represent robot poses (x, y, θ), and no outside influence, the average position of the robot will be s(k+1) = s(k) + Au(k+1).

As we have already discussed the particle filter side of things, this is also where we need to introduce the concept that our position shifts u(k) are noisy. In order to make our probability distribution truly a distribution, the idea is to have each particle updated both strictly with u(k), and with a random amount of process noise Qprocess.

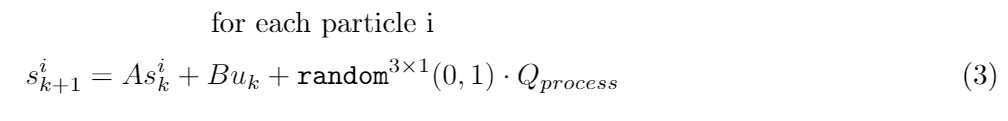
Where random generates a vector of 3 elements given random values according to the normal (float) distribution with mean 0 and st.deviation 1. Note that Qprocess is a representation of the noise in PICO's odometry, and hence a correct value will have to be measured, obtained from simulation settings (as a substitute to experimentation), or approached through tuning. As it is a compounding problem to try and dynamically calibrate noise covariance, this is out of consideration due to complexity alone - it would be like bringing another two smaller SLAM problems into the original SLAM problem.

The result of implementing (3) is that our particle filter - without any further logic - is an n-sampled representation of the motion law (1). Each timestep has the particles of our cloud spread out further, while adhering to the dynamics of u with each timestep. In other words, (3) implemented into a particle filter is an answer - but not a good answer - to the question `Where is my position, relative to my surroundings`.

Now we consider the other probabilistic law in SLAM, which just so happens to answer the other question posed at the start of this section;

Where we need to quickly introduce the concept of a landmark or feature. Within the confines of this project, it suffices to say 'corners', but in a more general sense: a landmark or a feature is something that the robot's sensors and feature recognition software can spot. Ideally, this is something that a robot can reliably and somewhat precisely pick out from its surroundings, but that is not formally part of the definition.

The law in (4) is known as the measurement model in literature. It talks about the probability that we make an observation z at time t, given that the robot has pose s(t), lives in the world w (which is a list of landmarks/features the robot can see), and that it has had some correspondence h(t) (which is an observation that at the least contains an identifier for a certain landmark, and likely also some measurement depending on the robot's sensors). With other words, it is an answer to the question `Should I see this?`, which is directly related to `what are my surroundings, and what are they relative to me?`. We're almost there!

Note that we have not introduced any notion of persistent landmarks; the set w can theoretically expand infinitely. The reason that this matters will become apparent shortly, when we combine the two probablistic laws (2), (4) into a probabilistic definition of our SLAM problem: