PRE2019 3 Group16
Group Members
| Name | Student Number | Study | |
|---|---|---|---|
| Efe Utku | 1284290 | Applied Physics | e.utku@student.tue.nl |
| Roel den Hoet | 1248170 | Computer Science | r.d.hoet@student.tue.nl |
Percentage Division of the Output Work:
Efe - 85%
Roel - %
Presentation Link
Problem Statement
Infectious disease outbreaks have been a fundamental threat to humanity since its history. There are various settings, worldwide, that might lead to an epidemic or a pandemic due to bacterial, viral etc. reasons. Although these outbreaks have various impacts on the society; one of them is the failure of health systems. Every region has its own medical capacity; limited by their number of beds, doctors, nurses etc. and during an outbreak, a fast spreading disease may lead to an overwhelming number of patients seeking medical attention. Here, we suggest a drone operation that can be used in viral outbreaks for remote testing and collecting nasopharyngeal specimen from people living in preselected disease-prone regions and communities. By decreasing the effective contact rate significantly and keeping precise track of more people in less time compared to current strategies; we aim to decrease the consequences of an outbreak on the community.
Subject
Communicable diseases can be defined as diseases with the possibility to be transmitted from one individual to another and they can be “classified by a variety of methods: by clinical syndrome, mode of transmission, methods of prevention…”. (Tulchinsky et al., 2014) As, Tulchinsky et al. points out despite the advances in technology and medical sciences; they are likely to remain a challenge for public health. These communicable diseases also affect community life; so, starting from their effects on individuals, in time, they spread over and might cause epidemics/ pandemics. Epidemics are defined as local infectious disease outbreaks that occur in a community or region. Thus, collective problems of each individual start to affect the society altogether. The major impacts of these outbreaks are reflected on the daily life of community members as economical, social and political issues. The economical problems are mostly due to measures taken to prevent the spreading of the disease; e.g. working, transportation and gatherings in public areas are halted, borders are closed, import/ export limitations. Social problems arise from the difficulties faced by the society as economical and state related problems begin to affect masses in time. Inevitably, social tensions lead to political issues and the occasion becomes a positive feedback cycle of problems. An example of a central problem emerging in dangerous situations is the failure of health systems; faster the disease spreads more people need medical attention in the short term. In addition, medical sector, like other sectors, has finite resources and limitations; so, hospitals can be overwhelmed, and health systems might fail to provide adequate attention. “This threat may increase as infectious diseases evolve and escape current human-developed control mechanisms.” (Tulchinsky et al., 2014)
To minimize these impacts states must keep an up-to-date record of regions that are prone, people who might be infected and people who are more susceptible to infections; because in the bigger picture the main problem is fast identification and tracking of reported cases. Only this way, measures and intervention policies can be effectively applied; so, the spreading rate can be reduced and the distribution of new cases per day can be minimized. The most efficient way to do this is to detect “local sources” of an outbreak. These are the people who are not infected by an infectious person inside the community; one can call them “first generation” of infected people. Also, here detection refers to subjecting them to a test which gives positive/ negative outcome indicating their disease status. Then, by reinvestigating the timeline of the sources; the spreading can be blocked to some extent; conditional on the mode of transmission of the outbreak. However, this approach is most of the times too difficult as reinvestigation of the timeline is merely “rational guessing” and some diseases have radically high transmission rates e.g. mostly modelled by exponentials. So, it can be difficult to distinguish between first and secondary cases. Thus, instead of focusing on actual “local sources”, states focus on all cases as being local sources. As time progresses, this also becomes increasingly hard to control due to the number of cases and it has cost and logistic complications within. Because every identification means a test and every test means a possible source going to a hospital, laboratory and contacting crowds including doctors and nurses.
So, we suggest an alternative strategy; to self-collect samples and use aerial drones for specimen collection and case identification. The core aim of the drone operations is to provide a faster logistic solution for case reporting, to increase the number of tests that can be conducted in a day and to make tests more remote, so less people are contacted in the process of testing. Hence, more time is provided to act and take precautions regarding the spread; such as increasing the capacity of hospitals and strengthening the health system.
This subject is going to be investigated in terms of its’ effects on different stakeholders and the its’ numerical impact on the way the disease spreads. The later, technical, part also consists of 2 components. First one is the mathematical model describing the population dynamics with and without the drone strategy, and the second one is an optimization problem to get a realistic point of view on the possibilities of this strategy.
Objectives
Deliverables
The list of the deliverables and their explanations are given below.
Mathematical Model and Simulation of Population Dynamics
An interpretation of the "S-E-I-Q-H-R" compartmental epidemiological model describing the population dynamics of a community. The model is given by a system of ordinary differential equations.
A MATLAB script for simulating mentioned mathematical model; which is used to investigate the impact of the drone operation on the spreading of the disease.
Optimization of drone fleet and operation base location
Users
Primary Users
The primary users of our product are the companies that are dealing with a viral outbreak. These companies have to find a good balance between being able to operate while still protecting their employees from unnecessary exposure to the disease. If they try to protect their employees too much, their company profits will suffer from the lack of employees that are still able to work in the company. However, if they let everyone come to work anyways, the employees might infect each other, which also leads to reduced profits. With our project, companies can find the employees in their company that are infected with the disease and isolate them from the rest of the company, while not isolating the employees that are healthy to make sure that the company can still continue making profits when possible.
The other primary users of our products are governments and municipalities that are dealing with a viral outbreak. These users are interested in keeping as many people healthy as possible, by identifying the infected people and isolating them from others. Our product can be used to keep the amount of infected people to a minimum while avoiding a complete lock down situation. If the infected people are found quickly, the impact on the healthy part of the population can be very low. By targeting the people that are most susceptible to the disease first, our product can stop the spreading of the disease in an early state.
Secondary Users
The secondary users of our product are the people that will be tested by their company or government. For the people that are susceptible to the disease, our test can either give them confirmation that they are indeed sick, in which case they need to stay home to avoid infecting other people, or it can tell them that they are not yet infected by the disease, in which case they can safely go outside without having to worry about infecting other people. This can make the infection rate much lower, as asymptotic people can also be identified in this way. Without this test, the asymptotic people would go outside and infect other people without knowing that they are sick.
Society
For more than 500 years, big epidemics have killed millions of people from all over the world. These epidemics do not only harm the people directly, but also damage the economy wherever they strike. The influenza epidemic from 2009 caused more than one billion dollar in damages to the economy of the United States, according to Yang-Woo et al., which included medical costs but also indirect costs of this epidemic. For society, the impact on people's lives during such epidemics are massive. Normal daily life becomes almost impossible during this time due to governmental lockdowns and the fear of being infected while outside. With our project, we want to limit the impact of an epidemic outbreak on normal daily life by quickly finding the people that are infected and isolating them from the healthy people to decrease the spreading of the disease. This does not only apply to the people that are showing symptoms of the disease, but also to asymptotic people, who are infecting healthy people without knowing that they are sick.
Enterprise
To produce the drones needed on a large scale, drone companies need to produce more drones than they do now, which might enable them to get cheaper parts for buying them in bulk. This would make the drones a bit cheaper as well. These drone companies can use the profit they make to do more research for drones, so that the drones can be improved as well. This can help decrease the effect of big pandemics on the drone companies by helping them economically, so they will still be able to operate. If our project gets rolled out at a large scale, we will also need a very big number of nose swabs and corresponding plastic containers that can be used to carry them. This can help these factories as well by providing them more income.
Description of the Operation
Pre-Test Phase
Selection
This phase is as essential to the operation as the testing phase is. Because, the success of the whole operation is dependent on the sample group of people who are tested. Testing of regions and areas that are not of neccessary would lead to wasting of resources. Considering the resource limitations of epidemics/ pandemics, the reflection of these wasted resources on the society would be of critical importance. So, the goal of this phase is to optimize the usage of resources by limiting the operation zones. Only by this way the overall success of the tests would be greater, so more people can be isolated and identified as exposed/ infected.
There are methods to evaluate how prone a region is both prior to the outbreak and during the outbreak. Both would require huge amount of data processing and AI and ML solutions would be required. As these techniques are not in the scope of this project, they are not going to be discussed in detail, but this section will serve as an outline to list the possibility of such methods.
A major approach to this issue is to use “Predictive Analysis” and more specifically “Health Predictive Analysis”. Ibrahim et al. (2017) gives a fine descriptive framework by evaluating the factors leading to spreading of diseases. They identify 4 main categories to start from; physical network, geography, clinical studies and social media. They also argue about the correlation of these categories and how they relate to “dissemination factors”. The drone operation will start in case of an outbreak and act as a local solution. It can also be used simultaneously in multiple regions to be considered as a global solution. Thus, the geography category can be neglected as it is the category related to ecological factors such as temperature and humidity. Because, the operation area can be seen as having homogenous ecological features. As to prioritize the other categories regarding the scope of the drones, we consider “physical network” to be the most important factor. Physical network refers to features such as population density. Andrick et al. (1997) point out that viruses need a third-party aid to mobilize themselves and to infect another host. This statement emphasizes the importance of physical contact and especially “effective contact rate” which is a direct parameter in the mathematical model. Second important category is “clinical studies” which outlines the awareness of districts and neighbourhoods regarding outbreaks and health care. This category can also be thought as a probability of how likely an individual from a specific zone can be infected and infect other people. The last category is social media which uses factors like geo-mapping. This can be seen as an additional category for real time double-checking of the contagion. It utilizes social media activities of areas and can be modelled easily by the ratio of “Negative Update Posts” to “Total Number of Live Feed” according to Ibrahim et al..
The data related to these categories can be collected in a periodic fashion to form databases by the help of national governments and private companies. The next step is to process the data. Gakwaya et al. (2019) proposes several methods to do so; Likelihood, Improved Expectation Maximization and Ensemble Neural Networks. For the sake of this project we consider the latter to be the appropriate one. “Ensemble classifier is a ML technique, which has been used to learn and recognize complex patterns.” In their paper they give an illustration of the algorithm for Ebola virus, it can be extended to SARS-CoV-like diseases in our case. It takes a definition of the virus as an input which are the classifiers mentioned in the previous paragraph. Then, the data is processed in two categories, “confirmed cases” and “suspected (unconfirmed) cases”. The yield can be used identify prone regions and, by updating the data regularly and including new cases, it can be used to identify suspected people to be tested .
In addition, there are several symptomatic criteria to identify individuals as probable cases. People matching these criteria can also contact the authorities performing the operation, in request to be tested. The major symptoms for SARS-CoV include: “persistent fever, myalgia dry cough, headache and dyspnoea” (Hui et al., 2003). If they also have a history of possible “effective contact” they may qualify. Otherwise, the requests for tests can exceed the test kits in the repository.
After people are identified to be tested using these methods, they can be informed by calling or by other means of communication like phone applications. Although, we don’t actually propose a way to inform people for now, we sketch a few possibilities. This is because not everyone can be accessed in the same way; for example, there are people without smart phones. However, it should be noted that application usage is our preferred way as it can also be used to notify people regarding their test results and update them on daily basis by giving recommendations (suspected areas, health care routines etc…).
Operation Bases
The construction and preparation of the operation bases is also a procedure that needs to be performed before the start of testing phase, as the facility needs to be ready for processing any sample that they receive; and after the selection of regions/ people that are going to be tested because the location of the bases are selected accordingly. The selection of bases' location is treated as a logistic problem and solved using optimization algorithms. By this way, most suitable locations can be identified to achieve the fastest working specimen transportation/ testing routes. The need for number of bases increases with the estimated number of tests that will be performed and also affected by the topography and complexity of the terrain/ urban environment.
The bases can be formed using pre-fabricated building techniques, companies such as CID Steel Building, Inc. and PortaFab and Vanguard Modular provide such capabilities under the name "modular laboratories" and also offer different sizing and configurations. Another advantage of using pre-fabricated structures is the possibility to relocate them; meaning once they are constructed and used in an outbreak, they can be stored to be used in another situation. In addition companies like STARRCO can also provide "isolation rooms" and "negative pressure rooms", which are vital for disease outbreaks as they can transform the same facility to an "emergency hospital". This feature is especially critical in epidemic/ pandemic times when there is high demand for hospital beds.
Another need of the bases is the actual machines that perform the testing. There are a variety of techniques and machines that can be used, each having different duration, sensitivity, efficiency and ultimately price. ThermoFisher Scientific is one of the many companies providing these equipment. They have different options for versatility, sensitivity, efficiency etc... In the scope of this operation we think the most suitable machines would be "QuantStudio 12K Flex Real-Time PCR System", "StepOne™/ StepOnePlus™ Systems" and similar Real Time RT-PCR machines. The latter one is considered to be more productive in terms of simple-usage, duration and price; which is needed for fast test processing and increasing the number of daily tests. It is also easy to transport and configure considering its' 24kg weight and dimensions.
 "A photo of StepOnePlus System"
"A photo of StepOnePlus System"
 A sketch of a STARRCO Modular Room that can be potentially used to form base laboratory
A sketch of a STARRCO Modular Room that can be potentially used to form base laboratory
Test Phase
How Sampling is Performed
After notifying the selected people that they are going to be tested, an empty container with the right apparatus is sent to them prior to the collection. The container has a QR code representing the individual/ household. Normally, the containers are marked by waterproof pen; however, that might lead to confusion in the automated process of sample collection, so it is not used. The type of test and the size of the container depends on the outbreak, as different specimen and different test are needed for different diseases. In this project we are going to focus on viral outbreaks and more specifically SARS-CoV-like diseases. For such diseases, methods like PCR tests, negative antibody tests and virus isolation are currently approved and used by WHO. Also, it should be noted that each test has different procedures and confirmation times. RT-PCR methods are confirmed within 3-4 hours whereas virus culture methods can last 2-10 days. Each test has their own sensitivity, time and effectiveness implications for the whole drone operation.
So, depending on the disease, in this case mostly upper respiratory nasopharyngeal swabs are collected and processed. This sampling is also assumed to be the most effective sampling regarding the operation as it has relatively higher sensitivity for self-collected specimen. This is also noted by Jackson et al. as “self-swabbing at home is feasible for confirming Acute Respiratory Infection etiology” according to a 2015 study. The instructions regarding the collection procedure is also sent along the empty container to clarify any misunderstanding. An example text presented in the CDC website is as follows:
“Insert a swab into nostril parallel to the palate. Swab should reach depth equal to distance from nostrils to outer opening of the ear. Leave swab in place for several seconds to absorb secretions. Slowly remove swab while rotating it.”
According CDC, the specimens must be stored in a 2 to 8 degrees Celcius environment and the sensitivity of the test is maintained up to 72 hours in such conditions. During the transportation ice packs can be used to suffice this condition. Otherwise, -70 degrees Celcius cryogenic usage is recommended; which is not possible in non-medical facilities. The samples are then collected and transported to the selected clinical facility, base.
Approach and Return of Drones to Bases
On the day that the person is supposed to get tested, they get a notification from a phone application. This notification tells them that a drone will visit them today to collect specimen. A few minutes before the drone arrives, they get another notification that the drone is nearby. When the drone has arrived, the people will put their specimen in a plastic container marked with a QR code and their name. The drone will wait at the door until all specimen from the household is collected or until x minutes have passed since its arrival. The drone then leaves and flies to the next destination, either another person or the operation basis.
Drone (State of the Art)
The drones that are available on the market can be divided into several categories, each with different price ranges and different uses. The drones under €500 are usually toy drones that should not be used for professional work, so for this project they are not interesting to look at. Drones that are more expensive are usually used by professionals, with high quality cameras and more intelligent flying options. There are a lot of options in different price ranges here, such as the DJI Mavic 2 Pro (https://www.dji.com/mavic-2) for about €1500 and the Intel Falcon 8+ (https://www.intel.com/content/www/us/en/products/drones/falcon-8.html) for about €30,000.
For our project, we need a drone with a good battery that can fly in a city environment autonomously without any problems. The drone should also be able to carry the specimen containers safely to the operation basis. The drone with the highest flight time is the DJI Mavic 2 Pro, which can fly for 30 minutes at 25 kilometers per hour. For our project, this would mean a maximum range of 6.25 kilometers from the drone base where we can operate. However, this drone is not made for carrying objects.
Drones that are made for sample transportation, like the Matternet M2 (https://www.engineeringforchange.org/solutions/product/matternet-m2/), which can carry a payload of 1 kilogram for a maximum of 20 kilometers, are more interesting for our project, since these drones are made for the same purpose as the drones we need. This drone also fits the requirement of being able to fly autonomously to the destination. These drones can carry a maximum payload of 2 kilograms, but carrying more than 1 kilogram will negatively impact the range of the drone on a single battery charge. The drone uses GPS and other sensors to find its way to the destination given by the user.
Population Dynamics
Mathematical Model
Use of mathematical methods have proven to be a successful way for estimating population dynamics. This approach dates back to mid 18th century and Bernoulli’s works on smallpox. He is also the first one to clearly define some of the most crucial epidemiological parameters, which are still used now. (Dietz, 2000) Although these methods are being improved since then, his work has also been essential to the theory of disease control. (Smolinski et al., 2003) Disease control theory refers to the applied intervention policies regarding infectious diseases and their systematic study as mathematical models. These models, consisting of various parameters, provide the framework to investigate how each intervention policy will affect the dynamics of population groups in case of an outbreak.
Based on the drone operation intervention policy mentioned in this report; here, we propose a compartmental epidemiological model to study the impact of this strategy. Compartmental models are deterministic, helpful for simplifying the problem and hold an assumption that individuals in the same compartment have the identical characteristics; thus, mean values are used. The model we used is derived from the iconic “S-E-I-R” Model (Kermack et al., 1927), the model used in the study of Chowell et al. on early detection of Ebola virus and "S-E-I-Q-H-R" model of Safi et al. (2010) whose results are complementary to the core aim of our approach
We define a model where the population is divided into 6 compartments. Namely; Susceptible (“S”), Exposed (“E”), Infected (“I”), Quarantined (“Q”), Hospitalized (“H”) and Recovered ("R").
Susceptible group, S(t), is the people who can be infected at time "t", Exposed group is people who are infected but are asymptomatic, can't infect other people and can give positive test results, Infected group is the people who can infect other people and symptomatic. Quarantined people are the group that is identified as positive carrier of the disease, might be symptomatic or asymptomatic and can infect other people to some extent depending on the effectiveness of the quarantine; Hospitalized people are people who are infected and as a consequence of their condition need medical attention. Finally, Recovered people are the group who were infected and recovered from the disease after some time. It should be noted that in the model a parameter is used to describe the fraction of people who can become susceptible after recovery; yet, considering our case study SARS-CoV-like diseases; this transition is neither experimentally verified nor proved to be impossible.
The flow diagram of the model given below displays the transitions between the states.
And the corresponding differential equations are given as;
dS / dt = Π + ψR - λS - μS,
dE / dt = λS - (κ+σ+μ)E,
dI / dt = κE - (γ1+φ+μ+δ1)I,
dQ / dt = σE - (α+μ)Q,
dH / dt = αQ + φI - (γ2+μ+δ2)H,
dR / dt = γ1I + γ2H - (ψ+μ)R.
Where;
λ(t) = β(I+ηH)/ N
is defined as the “force of infection” by Safi et al..
μ, Π, κ, α, φ, ψ, δ1, δ2, η, γ1, γ2, β and σ are consecutively the natural death rate, recruitment rate, rate of development of clinical symptoms, hospitalization rate of quarantined (Q), hospitalization rate of infected (I), loss of infection acquired immunity, death rate of I, death rate of H, relative infectiousness, recovery rate of infected people, recovery rate of hospitalized people, effective contact rate and rate of being quarantined. The values of the parameters are defined such that they reflect the SARS outbreak of 2003.
In addition, the parameter σ is redefined to be proportional to the maximum number of tests that can be conducted in a day and the sensitivity of test. The sensitivity of the test is also a function of the sensitivity of the sample being used in the test. As the sample is self-collected it has uncertainty and that is written in accordance with the results of Jackson et al.(2015).
The model has the boundaries: (S(0),E(0),I(0),Q(0),H(0),R(0)) ∈ { (S,E,I,Q,H,R) ∈ [0,N^6 ]: S≥0, E≥0, I≥0, Q≥0, H≥0, R≥0, S + E + I + Q + H + R = N }
From these boundaries, in the limit t→∞ it can be proven that a Disease-Free Equilibrium and an Endemic Equilibrium exists for different initial conditions. More information regarding the global dynamics of the model is present in Safi et al. 2010 paper.
Significance of the Model
There are various epidemiological models present in literature. The reason for selecting this model is its approach to the impact of intervention policies. Safi et al. claim quarantine and isolation of individuals is "probably the first infection control measure in the history" and it has been proven to be successful in numerous "emerging and re-emerging human diseases" including plague, cholera, ebola, pandemic influenza... Gumel et al. (2004) also used variety of this model in their paper "Modelling Strategies for Controlling SARS Outbreak" right after the SARS outbreak of 2002 where more than 30 countries and regions were affected. So, it is a widely accepted model to demonstrate the impact of these control measures.
Our use of the model, however, varies from these studies in terms of the proportionality of some parameters. We use this proportionality to show the difference our drone based testing approach has in relation to the current testing approaches. First difference is due to the number of tests; by providing a faster logistic solution we assume that more tests can be conducted using a drone fleet. Increased number of tests is reflected in the rate in which individuals are quarantined. Because more tests mean more identification and faster application of the isolation measures. The second difference is related with the remote testing opportunity our approach provides. As potentially infected people go to the nearest laboratory, pharmacy or hospital to be tested, they might use public transport or any means of transport to go to the institution. Also in the institution they might wait in lines and contact with other susceptible people. So, in the best case scenario they only contact the doctor, nurse, medic and there comes the risk of infecting a medical personnel. Considering the incubation period of the disease, this risk is enhanced in each contact involuntarily. As to reflect this risk in the model, we vary the "force of spread" function. There, the parameter referred as the "effectiveness of isolation" counts for this effect. 0 means this risk is minimized and 1 means none of the remote testing strategies are used.
Furthermore, the models can be extended to include different kinds of tests. Different tests have different verification periods as mentioned, this property can be applied as a factor of the quarantine rate as well. In the operations and numerical analysis elaborated on this project, the tests are assumed to be RT-PCR methods that give results in the same day. Thus, the mentioned factor is taken as "1".
Model Parameters and Case Scenario
For the interest of the simulation a case scenario is identified. The parameters below aim to reflect a scenario of a SARS-CoV-2 outbreak in the Netherlands. Some values from the SARS outbreak of 2003 are used as studies indicate vast similarity between two diseases and they’re from the same family of Corona viruses. As there are many relatively-less population density regions and towns are present in the Netherlands and the drone operations are performed locally; the numerical simulation focuses on the population dynamics of a region of “20000” people. This value is also influenced by the statistics that 265 of 288 Dutch cities have a population in between 10000 and 100000. Furthermore, it is assumed that all the requirements of the mentioned drone operation are fulfilled; e.g. bases are formed in time, testing equipment is sufficient, all tests can be collected/ transported safely. Also; the population is homogenous meaning effective contact rate and other characteristics are same for every individual, and sensitivity of the testing procedure is constant (age-of-infection is not used).
The selected constant parameters and their values are below.
Initial Population = 20000
Π = 0.0101 * 20000 = 202; Calculated by the product of birth rate in Netherlands (2020) and the Initial Population.
μ = 0.0089; The mortality rate in Netherlands (2020)
κ = 0.156986 (Donnely et al., 2003)
α = 0.156986 (Donnely et al., 2003);
The above two values are of a Honk Kong study as no data could be found about Netherlands.
φ = 0.20619; (Chowell et al., 2004)
ψ = 0.001; No data is present about infection acquired immunity; however, absence of evidence does not indicate evidence of absence. Thus, an uncertainty factor of 0.01 is used.
δ1 = 0.04227; (Leung et al., 2004)
δ2 = 0.027855; (Chowell et al., 2004)
γ1 = 0.03521; (Chowell et al., 2004)
γ2 = 0.027855; (Chowell et al., 2004)
Mean contact rate = 0.9575; Calculated by the weighted average of contact rates of different age groups living in the Netherlands. The contact matrix data is gathered from S.5 Appendix of Mossong et al. (2008)
β = Mean contact rate * Transmission Risk;
Transmission Risk = 0.20; Estimated according to the present data on β values of investigated models.
Sensitivity of the test = 0.70; (Al-Tawfiq et al., 2020)
Sensitivity of the sampling = 0.782; (Jackson et al., 2015)
Below are the parameters that can be varied to investigate the impact of different strategies.
Duration of a single test = 1;
Real Time RT-PCR methods and rapid diagnostic kits are assumed to be used.
Testing Rate = (T/N) * Duration of a single test;
Testing rate is defined as the number of tests divided by the total population (T/N) times the duration of a test. It reflects the maximum number of tests that can be performed rather than daily test number. In example, testing rate of 1 implies everybody is tested everyday. As of March 25, 2500 daily tests are being conducted in the Netherlands. T/N = 2500/17180000 = 0.00014552.
σ defined as: Sensitivity of the test * Sensitivity of the sampling * Testing Rate;
η as the effectiveness of isolation e.g. 0=perfect intervention;
Results of the Simulation
In this section, several scenarios obtained for spreading of SARS-CoV-like diseases in the Netherlands are numerically simulated using MATLAB and the initial conditions above. These scenarios display the impact of in-house testing strategy on the spreading of the disease. In addition, number of acute care beds is also displayed in the graph to get a view of the bigger picture. According to the latest OECD data, Netherlands has 3.32 beds for 1000 inhabitants.
Github link to the MATLAB Script: [1]
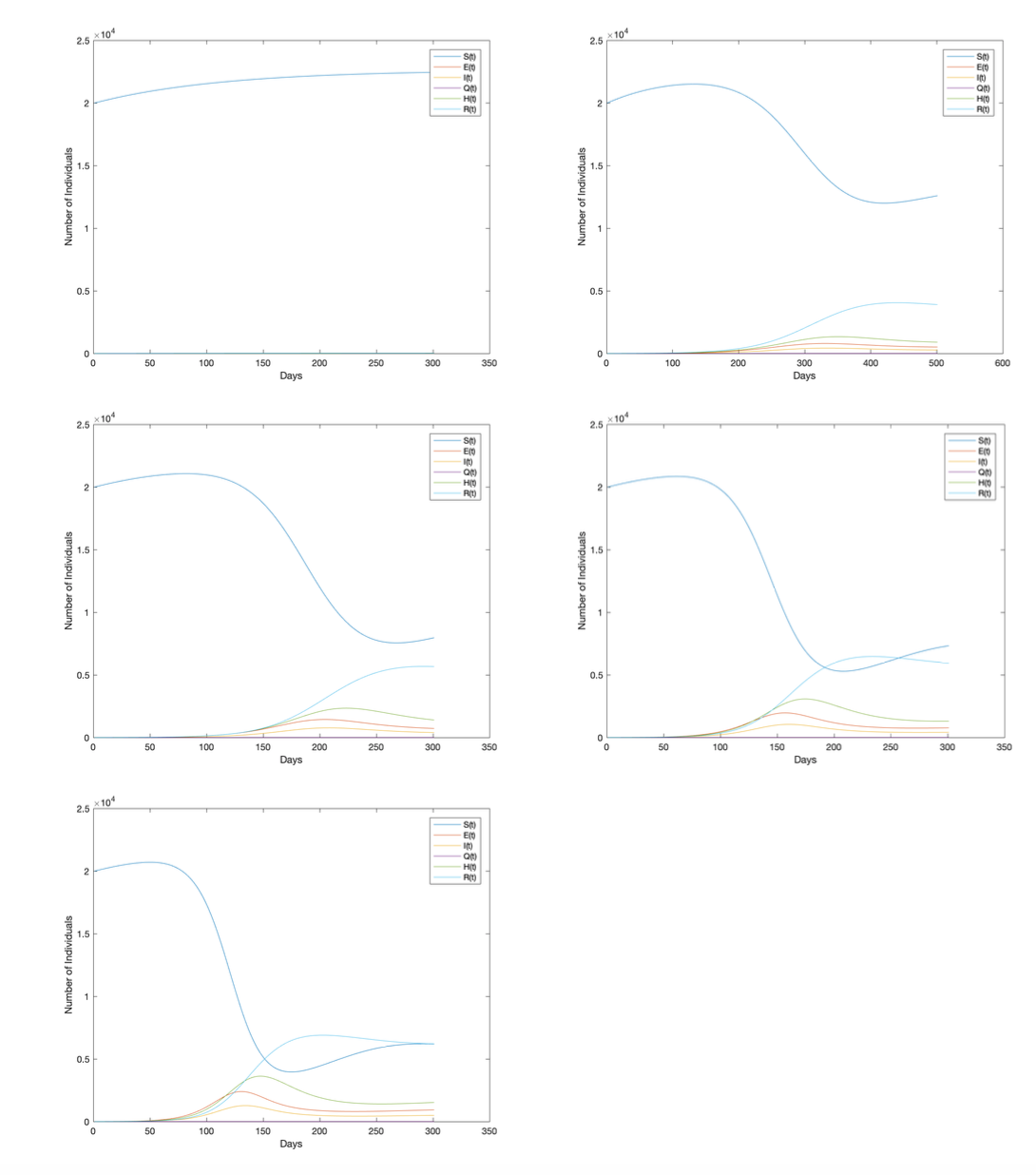
First Scenario: Varying η for Evaluating Remote Testing
As more people are subjected to tests in their house, the relative infectiousness presented in the "force of spread" is varied between 0.2 and 1 with incrementation of 0.2. Although empirical evidence is required to understand the exact impact and select a definite value; varying the η parameter demonstrates the impact and significance of the proposed strategy.
Furthermore, the initial conditions are based on the emergence of Covid-19 in the Netherlands. According to RIVM, 6412 identified cases were present on 25 March. Thus, 6412/17180000*20000 = 7.4645 is rounded towards positive infinity and the initial value for Infected group is selected to be 8. As a result,
S(0) = 19992,
E(0) = 0,
I(0) = 8,
Q(0) = 0,
H(0) = 0,
R(0) = 0 are the initial conditions.
Above figures show how different η values affect the overall distribution of each group where the other parameters are held constant. With top left being η = 0.2, top right 0.4, middle left 0.6, middle right 0.8 and bottom 1. It can be seen that lower η values reduce the transmission speed of the disease and yield lower peak values for E(t), I(t), Q(t) and H(t). Also, low η values shift the peak away from the origin, meaning the peak value is reached in a further date. As a result, the curve flattens. Top left graph also demonstrates for critically low η values the transmission rate is quickly damped and the chance of an epidemic is eliminated.
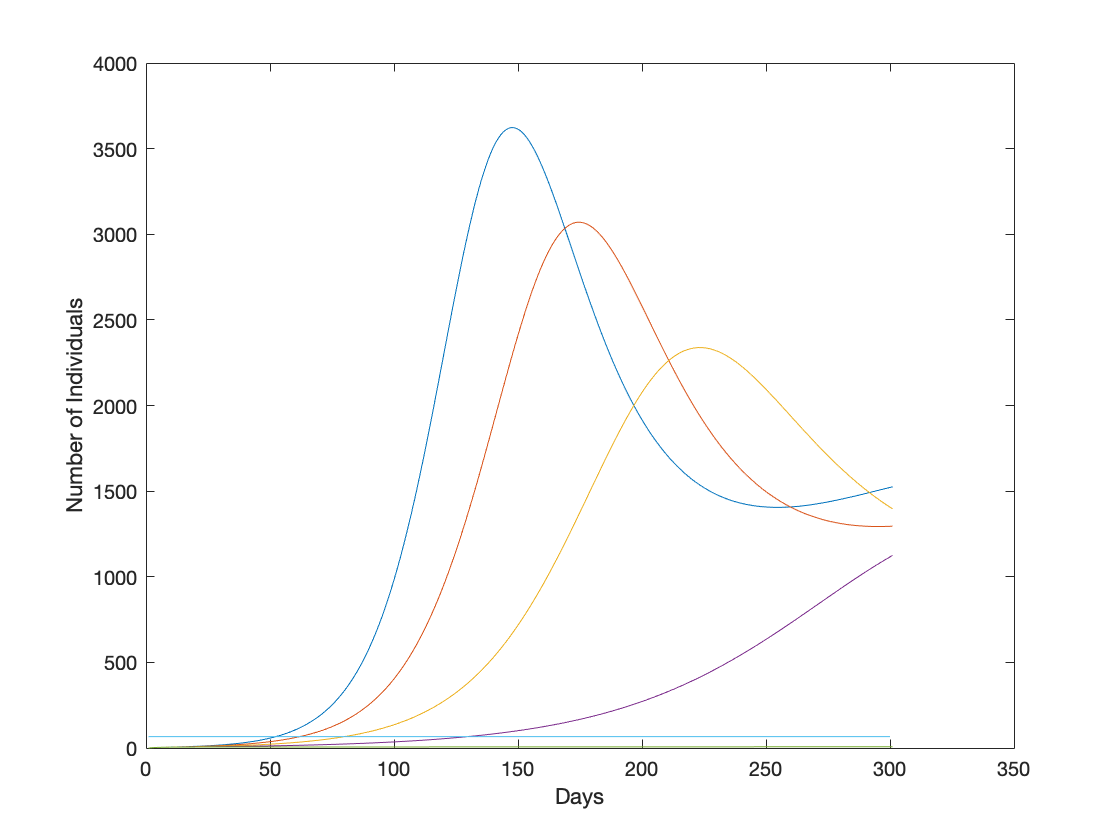
The figure on the left compares the H(t) values of each η value (from left peak to right; 1, 0.8, 0.6, 0.4 and 0.2) and the straight blue line shows the bed capacity of hospitals for a population of 20000, which is 66.4. η values higher than 0.2 always overshoot this capacity for these initial conditions. It is not clearly visible, yet the green curve below is the occasion where η is 0.2. In addition; the curves overshooting the bed capacity, in reality will be steeper and sharper as the effect of this overshoot is not represented in the model. Once this limit is exceeded, the needed attention can’t be given by the medical personnel causing more mortality and failure in the health system. A recent example would be Italy in 2020 Covid-19 pandemic. It must be noted that this evaluation is based on the assumption that no additional measures are taken, as in reality the product of this occasion would be far more complex.
Reflecting these results back to the drone operation; lower η values can be reached by effective quarantine measures and a way to reach that is to use remote testing operations such that the possibility of spreading the disease in any hospital or testing environment is reduced due to lower number of people outside and as a consequence less dense hospitals. A flattened curve also means medical resources can be used more efficiently and more people can be treated in a successful, more attentive way. By this way a country can overcome an epidemic/ pandemic situation with minimal damage to its’ medical capacity and economy; therefore, minimal damage to its’ citizens and inhabitants.
Second Scenario: Varying Initial Conditions for Evaluating the Effectiveness of the Operation
Figures above show the realizations for different initial conditions where the initial infected population is varied as 10, 20, 50 and 100. The η values are 0.2 for left and 0.4 for right figure.
For η = 0.4, it is clear that the peak of the curve shifts towards the origin while keeping the width almost same. This is as expected, because more infected people in the beginning would cause more people to be infected in a shorter time and as the intervention factor η is constant for all curves the peak value and trend doesn’t change. However, again as mentioned above, higher I(0) also causes the overshoot to happen in a closer date; so, health system failure and related costs are amplified in reality which is not displayed in the graphs. This commentary on the right figure is also similarly applicable to higher η values thus, they are not included above.
For η = 0.2, the damping is still valid in general, hence the overshoot doesn’t happen in this realization for I(0) = 10, 20 and 50. When I(0) is 100, it can be seen that an overshoot occurs and to not exceed this limit higher intervention measures need to be taken. In theory lower η values would compensate this difference; yet in practice this doesn’t seem achievable unless lockdowns and similar higher authority intervention measures are taken. As those higher intervention measures are also applicable to any other realization that can be made, and it is not in the scope of this proposed strategy they are not treated. So, the conclusion is that for high I(0) values this operation alone is not adequate but can be used to improve the taken measures.
Third Scenario: Varying T/N for Evaluating the Impact of More Tests
Last scenario to be evaluated is the impact of increased number of tests as the drone operation intends to increase the number of daily tests as well by providing a logistic solution. The figure above shows 10, 100 and 1000 thousand times more tests being performed for η = 0.6 and I(0) = 8. The result is that more tests shifts the peak to a further date, but the peak value and width of the curve is also increased. An explanation would be that more tests result in more validated cases, so both the peak and width increase with the test number. Shifted peak is related to the effectiveness of intervention as more cases can be identified and quickly quarantined. In short, Q(t) increases as I(t) decreases. The increased peak value and width is related to the interpretation of the used model. The rate of being quarantined is proportional to the number of tests and quarantined individuals are transferred to the H(t) compartment according to the model, so peak value and width increases with tests as well. These trends are likewise for different η values, so they are not presented here. As a summary, though some extent of the relation is covered by the model we believe that the relation between test number and hospitalization is not reflected in depth detail.
Also, it must be noted that increasing the test number is essential to understand the dynamics of a disease, understanding the dynamics helps to better understand what measures are needed to be taken; so, the outbreak can be controlled. If one doesn’t test anyone then the official number of infected individuals would be 0.
Maximizing the number of tests
Increasing the number of tests leads to better understanding and control over the spread of a disease and thus is of great importance. However, this is not an easy task given the current limitations of drones and also the limited budget and base locations for such operations. It is important to be able to get the optimal number of tests in any situation. Realistically, in the midst of an outbreak, the operation bases will not be optimally located at all and the drones quantity and quality will be far from ideal. This is why it is so important to develop a system that computes exact routes for all the drones so that the total number of people that they serve collectively in a given period of time is maximized.
This type of problem is NP-complete, i.e. with current technology it can never be solved optimally even for relatively small instances. However, the optimal solution can be closely approximated. When designing such system scalability is essential. It should be able to handle both small areas with a lower population and a small number of drones by using more exact algorithms and approximating closely the optimal solution, and also large areas of millions of people with fleets of hundreds of drones. For such large instances, the best and probably the only solution right now would be using an optimization algorithm.
An optimization algorithm is essentially an iterative procedure that starts with some initial guess solution and aims to reach a better solution or ideally the optimal solution to the given problem. We decided to use for our simulation the method called simulated annealing. It models the physical process of heating a material and then slowly lowering the temperature to decrease defects, thus minimizing the system energy. At each iteration from the current solution, a neighbour solution is created by making a random change in some of the routes of the drones. The distance between the two solutions, i.e. the difference in the total number of tests, is based on a probability distribution with a scale proportional to the temperature. The algorithm accepts all solutions that increase the number of tests, but also, with a certain probability, solutions that decrease the tests. By doing that the algorithm avoids being trapped in local maxima, and is able to explore globally for more possible solutions. An annealing schedule is selected to systematically decrease the temperature with each iteration and thus reduces the extent of its search to converge to a maximum.
In order to be able to use this system in different situations, other than the obvious adjustments that can be made, we add the option to set the speed, max flight time, range, time until full charge, max number of tests that can be carried and average service time per test for the drones. We further increase the complexity of the problem by including the charging of the drones into the calculations and adding the option for the drones to switch bases, i.e. start from one base and deliver all gathered tests to another base. Considering all of this, it would be very difficult to come up with any good approximating algorithm, but it is not a barrier that simulated annealing can’t overcome.
The route of a drone is represented by a list of sets of people. The idea is that each set contains all people that the drone will cover before needing to recharge and deliver the tests to a base. For each set, there are also the start and end bases, possibly different. This way we make the random changes that the simulated annealing does simpler to execute: it would be simply adding/removing a person from a set, changing a destination base etc.
However, we are talking about sets but we want the drones to have an exact path drawn out for them. To achieve that we look at each set as an instance of the travelling salesman problem, which is another NP-hard problem. We want to find the shortest tour visiting all people, including the bases. Note that if the start and end bases are different we can simply add an imaginary destination that is at distance 0 from both bases so that we can then remove it from the resulting tour and guarantee that we have the two bases as ends of the path.
For the travelling salesman problem, there are a few relatively fast exact algorithms that find the optimal solution that could be used in cases when the drones have a small capacity or just can’t reach more than 10-15 people in one go. However, this algorithm is to be used as many times as possible, so, for this reason, we chose one of the better approximating algorithms - Christofides algorithm, that can handle more than enough destinations even for the best drone on the market. The Christofides algorithm combines a minimum spanning tree with minimum-weight perfect matching. This gives a solution which is at most 1.5 times the optimal.
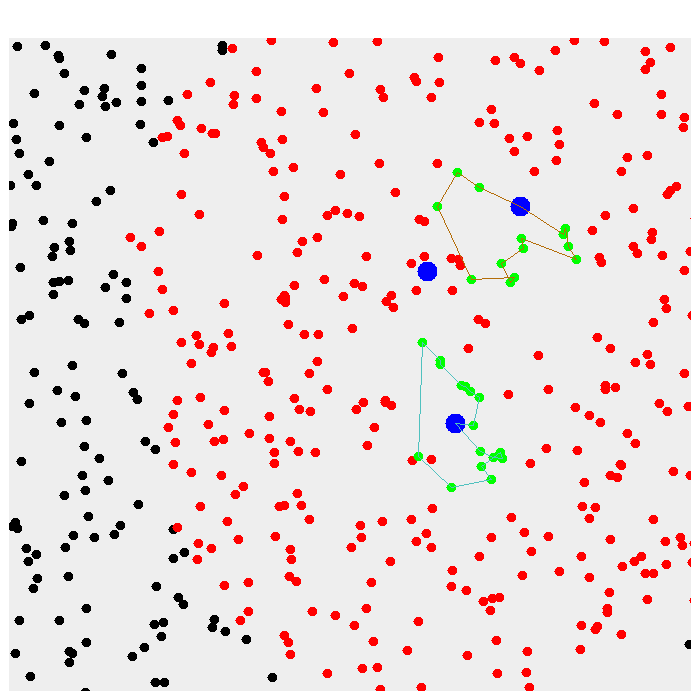
Our simulated annealing algorithm can start with a random, greedy or even empty solution. The greedy solution is always picking the closest person to the drone to test, recharge (in the closest base if allowed) when it can’t reach any more people and go out again until the given time is over. Below can be seen results from using the greedy algorithm, then from using it for the simulated annealing, and finally results from simulated annealing starting from empty solution:
Greedy (29 tests) Greedy with recharging (53 tests) Greedy with base changing (34 tests) Greedy with recharging and base changing (52 tests)
SA from greedy (36 tests) SA from greedy with recharging (57 tests) SA from greedy with base changing (37 tests) SA from greedy with recharging and base changing (58 tests)
SA from empty (35 tests) SA from empty with recharging (56 tests) SA from empty with base changing (33 tests) SA from empty with recharging and base changing (59 tests)
On all images, the big blue dots are the drone bases and the other dots are the people - black for people not in range of any base, i.e. unreachable by drones, red for reachable people which are not yet visited by a drone, and green for people visited by the drones, i.e. tested. The lines show the routes of the drones, such that each drone has a unique route colour. For these simulations, there are three bases and two drones, one in the bottom and one in the top base. This is done for simplicity and better visibility of the results. Note that the settings of the simulation are such that the drone has enough time to go out twice to pick tests and to fully recharge in between, and also that each drone can carry at most 20 tests at a time.
Clearly, adding the option for the drones to recharge in the simulation increases the number of tests when the simulation time is bigger than the max flight time of the drones. However, it is important to notice that in the optimal solution it is very likely that drones don't always wait to fully charge and when a drone leaves it doesn't always try to get close to the max flight time, so enabling the simulation to produce such solutions leads to better approximations although the complexity of the problem increases. Additionally, it seems that adding the option for the drones to go to different bases tends to lead to even better solutions. One of the reasons for this is that there are people between some stations for which drones usually wouldn't go because of the distance.
If executed properly, simulated annealing should be able to improve any solution as long as it is not optimal, so it is only natural that it improves the results from the greedy algorithm. As for the significance of the start solution for the simulated annealing, to a certain extent, it matters because starting from different points in the solution space could lead to a different local maximum in the end, but then again, if the simulated annealing is executed the right way, i.e. finds global maximum, it shouldn't really matter. In our case, the empty and the greedy solution give very similar results after optimization. However, when the instance of the problem is very big, it would be likely faster if we start from a non-empty solution as we skip some initial iterations. For such big instances, the greedy could also be too slow so then we might just generate a random initial solution. Also, when the problem at hand is to complex and there are doubts about the simulated annealing, one might generate different start solutions, run optimizations and then pick the best solution.
Above you can see an example of a bigger instance with 10 drone bases, 100 drones (capacity of 15 tests) and thousands of people. We use simulated annealing on an empty solution and show the optimization process up to 1000 tests. Simulated annealing can handle even bigger instances as long as there is enough time, and how much time that is depends on the way it is implemented.
Conclusion
Epidemics and pandemics are inevitable for communities/ societies and many major examples are present in the history. Earliest evidence of pandemics can be traced back to Justinian Plague of 6th century which caused devastating impact on the society and civilization as a whole. Also, earliest intervention measures can be traced back in history and can be identified as isolation and quarantine applications. Where infected people and potentially infected people are isolated away from the rest of the community. In the modern era, risk of a pandemic is reduced but it still exists, and it is a fact of our daily lives. The same applies for their impact on the society as they still have the probability to cause failure in the health system and cause great economic crises. There is also an advantage we have in this era. The use of effective testing strategies and tracing techniques give us the opportunity to identify (potential) cases and to isolate them before they spread the disease to masses. However, most of the testing strategies are dependent on one-to-one contact of medical personnel and individuals. Meaning in order to be tested, people need to go to laboratories, hospitals and other authorized institutions which causes them to possibly infect others in their way. This situation emphasizes the importance of remote testing operations. A recent example of such testing is drive thru testing used by countries like South Korea, a country successfully controlled the Covid-19 pandemic compared to other countries. This success of South Korea is not only due to remote testing as other intervention policies are also effectively applied. Yet, South Korean authorities also stressed the importance of this testing strategy and fast case identification.
Throughout the sections above, we outlined an alternative remote testing approach via use of drones. Which can be considered as an eco-friendlier approach than drive thrus. Because of the fact that same amount or possibly more tests can be conducted without using cars and causing traffic congestion. The drone operation starts with an initial Pre-Test Phase, where prone regions and possible infected people are identified using Big Data and algorithms. Then, by use of optimization several locations are selected to be places of drone bases. These bases are constructed using prefabricated modular laboratories and equipped just like other hospitals/ labs with the required testing machinery, facilities and most importantly personnel. After the Pre-Test Phase, identified people are contacted, preferably by smartphone applications due to reasons mentioned earlier and are sent specimen collection kits. So, these people can self-collect specimen. An optimization method, provided in the Maximizing Tests section, then draws possible efficient routes for the drones to collect and transfer specimen to bases. At the end of each operation day, tested people are again contacted regarding their result and they receive recommendation for quarantine. As a summary more cases can be identified in a shorter period and in a more remote way; reducing effective contact and the weight on the shoulders of the health system.
Members of the society benefit from this approach as outbreak can be controlled faster so the overall effect is diminished, and they are not subjected to any potential risk for being tested. Also, the risk groups (elderly and people with existing medical condition) can receive better and more attentive medical care as health system will have less cases to work on. The states will minimize their damage by controlling the outbreak and reducing chances of economic collapse and medical system failure. Moreover, to make this drone operation possible companies can provide drone and technology assistance to hospitals/ laboratories. Such that these institutions can upgrade their existing facilities, resources and utilities; producing employment.
Some limitations also exist for this strategy as it is solely dependent on advancements in drone industry. An example for the limitations can be navigational issues in dense urban environments and residential zones. Also, it is possible that communication problems occur, and the route of the drones has to be redefined in limited time causing autonomy and efficiency problems in the operation. So, for the upcoming few years, it is better to consider this approach as a supplemental one to existing strategies and use it in coordination with them.
The presented MATLAB simulations also provide some insights to the scope of this strategy. First of all, the results of the simulations point out that drone operations can be efficient in terms of reducing the spread of the disease if practiced in a way that all requisitions are fulfilled, the requisitions are listed in the relevant sections. Also, an additional requisition is realized as a result of the simulation, that the timing of the operation is of critical significance. If operation starts after a threshold point, number of infected people is greater, it becomes similar to existing strategies. As a consequence, additional intervention measures are needed. The same outcome also arises if people don’t follow the recommendations, then the distinguishing features of remote testing is lost. A critique for the MATLAB simulation must be included here as well; the parameters and deterministic epidemiological model don’t reflect the actual complexity of the situation because pandemic times might be chaotic. Thus, the model can be improved by accompanying uncertainties, parameter variations, age-of-infection stochasticity and positive feedback mechanisms in the medical capacity.
Planning
Week 3: Make plan - research algorithm and model
Week 4: Research algorithm and drone - create model
Week 5: Implement algorithm - research drone
Week 6: Simulate algorithm - research drone
Week 7: Create presentation
Week 8: Give presentation
Milestones
Week 3: New subject chosen - plan made
Week 4: Research of algorithm done - model done
Week 5: Algorithm implemented and tested - drone research done
Week 6: Case example simulated - drone component list done
Week 7: Wiki finalized
Week 8: Presentation finalized
Task Division
Main Contribution
Efe Utku:
-Organizing and Structuring the Wikipage
-Written Problem Statement, Subject, Pre-Testing Phase, Testing Phase (How Sampling is Performed), Population Dynamics
-Performed/ Reported MATLAB Simulation
-Research and Briefing on all related subjects (33 listed reference)
Roel den Hoet - Research of algorithms, implementation and testing of algorithms, work on wiki page
Research, implementation, testing and description of algorithms
Weekly Contribution
The subject of the project and the structure of the group have changed in the third week; so, first three weeks are not included below.
17- 23/02/2020
Efe:
-Researched History of Epidemics/ Pandemics and their effect on societies [5 hours]
-Planned experimentation and modelling of population dynamics [5- 7 hours]
-Briefed the group about the new subject and drone operation idea [1 hour]
24- 01/02- 03/2020
Efe:
-Researched currently used intervention strategies and their impact, epidemic modelling, case studies [8 hours]
-Started simulating different epidemiological models for choosing the appropriate model (MATLAB) [10 hours]
02- 08/03/2020
Efe:
-Written Problem Statement, Subject [2 hours]
-Updated/ Finalized the WikiPage Template [0.5 hour]
-Researched Epidemic Modeling and Adjusting the Model [8 hours]
-Worked on MATLAB Simulation for Pop. Dynamics [5 hours]
Roel:
- Researched algorithms
- Updated the wiki page on User, Society and Enterprise
- Worked on simulating the spread of disease
09- 15/03/2020
Efe:
-Written Drone Ops., Pop. Dynamics Model [3 hours]
-Researched on test conducting, predictive methods for region/ people selection, existing datasets on epidemics [10 hours]
-Worked on MATLAB Simulation for Pop. Dynamics [5 hours]
Roel:
-Worked on Wiki page for Description of the Operation
- Worked on simulating the work of the drones
16- 22/03/2020
Efe:
-Updated Testing Phase, Problem Statement, Mathematical Model [3 hours]
-Researched on test conducting, intervention policies, effects of outbreaks, SEIQHR Model [8 hours]
-Worked on MATLAB Simulation for Pop. Dynamics [10 hours]
Roel:
- Updated Operation Description
- Researched Drones (State of the Art)
- Wrote drone section on Wiki
- Simulating annealing and visualization
24- 30/03/2020
Efe:
-Researched/ written Pre-Test Phase (How Sampling is Performed and Operation Bases) [4.5 hours]
- Constructed Flow Diagram of the model, adjusted the equations for Wikipage [0.5 hours]
- Performed MATLAB Simulation and reported results [6 hours]
-Written Conclusion [2 hours]
Roel:
- Rewrote User section of the wiki
- Updated drone section
- Visualization and wiki description
References
Academic
Al-Tawfiq, J. A., & Memish, Z. A. (2020). Diagnosis of SARS-CoV-2 Infection based on CT scan vs. RT-PCR: Reflecting on Experience from MERS-CoV. Journal of Hospital Infection. doi: 10.1016/j.jhin.2020.03.001
Chowell, G., Castillo-Chavez, C., Fenimore, P. W., Kribs-Zaleta, C. M., Arriola, L., & Hyman, J. M. (2004). Model Parameters and Outbreak Control for SARS. Emerging Infectious Diseases, 10(7), 1258–1263. doi: 10.3201/eid1007.030647
Chowell, D., Safan, M., & Castillo-Chavez, C. (2016). Modeling the Case of Early Detection of Ebola Virus Disease. Mathematical and Statistical Modeling for Emerging and Re-Emerging Infectious Diseases, 57–70. doi: 10.1007/978-3-319-40413-4_5
Dietz, K., & Heesterbeek, J. A. P. (2000). Bernoulli was ahead of modern epidemiology. Nature, 408(6812), 513–514. doi: 10.1038/35046270
Donnelly, C. A., Ghani, A. C., Leung, G. M., Hedley, A. J., Fraser, C., Riley, S., … Anderson, R. M. (2003). Epidemiological determinants of spread of causal agent of severe acute respiratory syndrome in Hong Kong. The Lancet, 361(9371), 1761–1766. doi: 10.1016/s0140-6736(03)13410-1
Gakwaya, N. J., & Priya, S. M. (2019). Contagious Diseases Prediction in Healthcare Over Big Data. Lecture Notes on Data Engineering and Communications Technologies Proceeding of the International Conference on Computer Networks, Big Data and IoT (ICCBI - 2018), 127–132. doi: 10.1007/978-3-030-24643-3_14
Hui, D. S.-C., Wong, P.-C., & Wang, C. (2003). SARS: clinical features and diagnosis. Respirology, 8(s1). doi: 10.1046/j.1440-1843.2003.00520.x
Ibrahim, N., Akhir, N. S. M., & Hassan, F. H. (2017). Predictive analysis effectiveness in determining the epidemic disease infected area. doi: 10.1063/1.5005397
Jackson, M. L., Nguyen, M., Kirlin, B., & Madziwa, L. (2015). Self-Collected Nasal Swabs for Respiratory Virus Surveillance: Table 1. Open Forum Infectious Diseases, 2(4). doi: 10.1093/ofid/ofv152
Katriel, G. (2013). Stochastic Discrete-Time Age-Of-Infection Epidemic Models. International Journal of Biomathematics, 06(01), 1250066. doi: 10.1142/s1793524512500660
Kermack, W. O., & McKendrick, A. G. (1927). A contribution to the mathematical theory of epidemics. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 115(772), 700–721. doi: 10.1098/rspa.1927.0118
Leung, G. M., Hedley, A. J., Ho, L.-M., Chau, P., Wong, I. O., Thach, T. Q., … Lam, T.-H. (2004). The Epidemiology of Severe Acute Respiratory Syndrome in the 2003 Hong Kong Epidemic: An Analysis of All 1755 Patients. Annals of Internal Medicine, 141(9), 662. doi: 10.7326/0003-4819-141-9-200411020-00006
Mossong, J., Hens, N., Jit, M., Beutels, P., Auranen, K., Mikolajczyk, R., … Edmunds, W. J. (2008). Social Contacts and Mixing Patterns Relevant to the Spread of Infectious Diseases. PLoS Medicine, 5(3). doi: 10.1371/journal.pmed.0050074
Safi, M. A., & Gumel, A. B. (2010). Global asymptotic dynamics of a model for quarantine and isolation. Discrete & Continuous Dynamical Systems - B, 14(1), 209–231. doi: 10.3934/dcdsb.2010.14.209
Smolinski, M. S., Hamburg, M. A., & Lederberg, J. (2003). Microbial threats to health: emergence, detection, and response:Washington, DC: National Academies Press.
Tulchinsky, T. H., & Varavikova, E. A. (2014). Communicable Diseases. The New Public Health, 149–236. doi: 10.1016/b978-0-12-415766-8.00004-5
Yaari, R., Katriel, G., Stone, L., Mendelson, E., Mandelboim, M., & Huppert, A. (2016). Model-based reconstruction of an epidemic using multiple datasets: understanding influenza A/H1N1 pandemic dynamics in Israel. Journal of The Royal Society Interface, 13(116), 20160099. doi: 10.1098/rsif.2016.0099
Yang-Woo, K., Seok-Jun, Y., In-Whan, O. (2012) The economic burden of the 2009 pandemic H1N1 influenza in Korea. doi: 10.3109/00365548.2012.749423
Website
CID Associates, Inc. (n.d.). Modular Laboratories. Retrieved from https://www.cidbuildings.com/modular-laboratories.html
Clinical Specimens: Novel Coronavirus (2019-nCoV). (2020, March 25). Retrieved from https://www.cdc.gov/coronavirus/2019-nCoV/lab/guidelines-clinical-specimens.html
Current information about the novel coronavirus (COVID-19). (n.d.). Retrieved from https://www.rivm.nl/en/news/current-information-about-novel-coronavirus-covid-19
Fisher Scientific. (n.d.). Retrieved from https://www.fishersci.nl/nl/en/promotions/applied-biosystems-stepone-steponeplus-real-time-pcr-systems.html
Health equipment - Hospital beds - OECD Data. (n.d.). Retrieved from https://data.oecd.org/healtheqt/hospital-beds.htm
Laboratories. (n.d.). Retrieved from https://www.portafab.com/laboratories.html
Modular Laboratories & Specialty Portable Buildings. (n.d.). Retrieved from https://vanguardmodular.com/specialty/modular-laboratories/
Modular, Portable Labs & Prefabricated Buildings. (n.d.). Retrieved from https://www.starrco.com/modular-clean-rooms/modular-labs/
(n.d.). Retrieved from https://worldpopulationreview.com/countries/netherlands-population/cities/
Netherlands Birth Rate 1950-2020. (n.d.). Retrieved from https://www.macrotrends.net/countries/NLD/netherlands/birth-rate
Netherlands Death Rate 1950-2020. (n.d.). Retrieved from https://www.macrotrends.net/countries/NLD/netherlands/death-rate
Netherlands now home to 6,412 coronavirus patients, up 15%; 80 more patients died. (2020, March 25). Retrieved from https://nltimes.nl/2020/03/25/netherlands-now-home-6412-coronavirus-patients-15-80-patients-died
QuantStudio 12K Flex Real-Time PCR System. (n.d.). Retrieved from https://www.thermofisher.com/de/de/home/life-science/pcr/real-time-pcr/real-time-pcr-instruments/quantstudio-12k-flex-real-time-pcr-system.html
StepOnePlus™ StepOnePlus™ Real-Time PCR System Upgrade - Products Home. (n.d.). Retrieved from https://www.fishersci.fi/shop/products/steponeplus-real-time-pcr-system-upgrade-2/15351295
Use of laboratory methods for SARS diagnosis. (2015, July 24). Retrieved from https://www.who.int/csr/sars/labmethods/en/
Wappes, J. (2020, January 24). Studies highlight nCoV similarity with SARS, family transmission. Retrieved from http://www.cidrap.umn.edu/news-perspective/2020/01/studies-highlight-ncov-similarity-sars-family-transmission