Ways to exite the string
Exitation by Electromagnet
Principle
Another way to exite the string is by using an electromagnet force on the steel strings. This force is created by the flow of current through a coil wrapped around a magnetizable core, creating an electro magnet. The force can be controlled by changing the current that flows through the coil. Because current can be controlled by speeds in the order of several Gigahertz, the flow can be controlled very rapidly.
Estimation for the maximum bow force on the string
Figure x shows the string on the moment it's being exited by the violin bow. The displacement of the string is called 'u', creating two angles α and γ. The string will be exited on position βL.
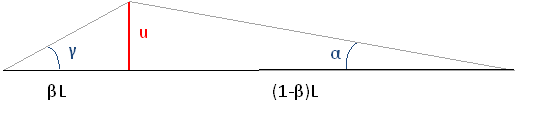 Figure x: The string exited over a distance u The force in y-direction is calculated with:
[math]\displaystyle{ F_y=sin(\gamma)A\sigma_{1}+sin(\alpha)A\sigma_{2} }[/math]
[math]\displaystyle{ \sigma=E\varepsilon }[/math]
[math]\displaystyle{ \varepsilon= {dL\over L_0 } }[/math]
[math]\displaystyle{ F_y = AE \left (sin(\gamma){\sqrt{\beta^2 L^2+u^2}-\beta L \over \beta L} + sin(\alpha){\sqrt{(1-\beta)^2 L^2+u^2}-(1-\beta) L \over (1-\beta) L} \right) }[/math]
The biggest static force acting on a string is the force when a short, thick string is exited. It is assumed that the length of this string is 20 cm and the diameter is 0.25mm.
The force acting on this particular string, exited over 0.5 cm, is about 40 N.
Estimation for the maximum dynamical force acting on the string
Since the string isn’t only exited statically but is being moved continuously, the static force calculated above isn’t the only force that has to be dealt with. The string should vibrate in a predefined pattern, and therefore big accelerations become important. The force needed to accelerate a certain mass m, is calculated using Newton’s second law of motion. This law states that this force is equal to acceleration times mass.
Since the acceleration of the string varies linearly over the length of the string, the acceleration (and thus force) should be calculated separately for every small segment of the string. This gives rise to an integral over the whole string. In order to do this, the string is divided into two pieces, being the part βL and the part (1-β)L.
This gives the following for the part βL:
[math]\displaystyle{ F = {ma} }[/math]
[math]\displaystyle{ F = \sum_{i=1}^{n}{m_ia_i} }[/math]
[math]\displaystyle{ F_1 = \sum_{i=1}^{n}{m_i\left( {da \over dx} x_i \right)} = \sum_{i=1}^{n}{m_i\left( {a \over \beta L} x_i \right)} }[/math]
[math]\displaystyle{ m_i = {\rho {\beta L \over n} A_{cross.sect.}} }[/math]
[math]\displaystyle{ n = {x \over dx} = {\beta L \over dx} }[/math]
[math]\displaystyle{ m_i = \rho A_{cross.sect.} dx }[/math]
[math]\displaystyle{ F_1 = \int_0^{\beta L} {{a A_{cross.sect.} \rho} \over {\beta L}} x \;dx }[/math]
[math]\displaystyle{ F_1 = {{a A_{cross.sect.} \rho} \over {\beta L}} \int_0^{\beta L} x \;dx }[/math]
[math]\displaystyle{ F_1 = {{a A_{cross.sect.} \rho} \over {\beta L}} [ \frac{1}{2} x^2 ]_0^{\beta L} }[/math]
And for the part (1-β)L:
[math]\displaystyle{ F_2 = {{a A_{cross.sect.} \rho} \over {(1-\beta) L}} [ \frac{1}{2} x^2 ]_0^{(1-\beta) L} }[/math]
Where:
a = The acceleration of the string on position βL
Across.sect. = The cross section area of the string
ρ = The density of the string
The total force needed to accelerate the string is given by:
[math]\displaystyle{ F_{tot} = F_1 + F_2 }[/math]
[math]\displaystyle{ F_{tot} = {{a A_{cross.sect.} \rho} \over {\beta L}} [ \frac{1}{2} x^2 ]_0^{\beta L} + {{a A_{cross.sect.} \rho} \over {(1-\beta) L}} [ \frac{1}{2} x^2 ]_0^{(1-\beta) L} }[/math]
This gives a total acceleration force of 6,25N when the following parameters are used:
a = 500 m/s2
Across.sect. = 5 ∙ 10-6 m2
ρ = 8 ∙ 103 kg/m3
The maximum total force, which is the force needed to give the string the maximum acceleration at the maximum position, is given by the sum of Fy and Ftot.
This means that the maximum magnetic force that is needed is about 50 N.
Feasibility
The calculation shows that a magnetic force of 50 N should be enough to exite the string in the desired pattern. Finding an electromagnet that generates this magnetic force is not a problem. However, the width of these electromagnets could be a problem, since there might not be enough space to place an electromagnet for each string separately. This problem could be solved by making the electromagnets on our own. The force that is generated in an electromagnet is only depending of the number of windings and the current through the coil. Since there is enough space underneath the strings, a long and tight electromagnet would work.
Another point is that the magnet of one string might interfere with another and disturb it’s magnetic field. However, this problem would be quite easy to deal with as will since a screen could be placed in between the strings or the control device a magnet could compensate for disturbances from the others.
Drawbacks
Despite the theoretical possibility to use electromagnets for actuation, there are two very important drawbacks in this concept. Firstly, the instrument will no longer be bowed although it sounds as such. In fact the instrument then will no longer be a bowing instrument, which was one of the main requirements. But probably the biggest disadvantage of this concept, is the quite illogical way of synthesizing the sound. To get the string in the desired vibration, this vibration should be known in advance. Getting this vibration would be no problem, since we can get it out of the model or simply record it from a real bowing instrument. But once the vibration is known, it has to be exited on the string using electromagnets, recorded using a sensor and then amplified before it is played. This is very strange since we already had the desired vibration when we started, and thus were already able to play it.
Conclusion
The conclusion about this concept is that it would work most likely and that every vibration pattern could be chosen. However, the big drawbacks that it is no longer a bowing instrument and that the synthesizing routine is very illogical, make the concept fail.
Actuation by piëzo crystals
Principle
A piezo actuator utilizes the phenomenon that crystals of certain substances expand when a voltage is applied on it or conversely, they give a voltage when pressure is exerted on the crystal. The name piezo is derived from the Greek word piezein, which means pressing. The concept for actuation by the piezo, is that the string is attached to a piezo element, which expands when a voltage is applied. The idea is that by varying the voltage, the movement of the string can be controlled, giving the desired vibration in the string
Feasibility
If the feasibility of this concept is considered, the combination of required force and deflection seems to be a problem. The reason is that piezo elements only enlarge a little, varying from a few micrometers to some tens of micrometers. There are piezo elements on the market that serve as a linear motor and have a maximum amplitude up to 100 mm, but again does not provide the required force. Another possibility is to use so-called piezo stacks. This a series of piezos allowing the maximum deflection to increase. However, this excursion is also just a little more than 1 mm for the required force, which is not enough.
Drawbacks
The main disadvantage of piezo actuation is that the deflection they give is not large enough. This problem is partly dealt with using a stack, but even then the deflection is not large enough to make the string vibrate in the desired shape. Furthermore, in this design the instrument will no longer be a bowing instrument
Conclusion
From the foregoing it can be concluded that it is not possible to get the string in the desired vibration using piezoelectric actuators. Also the instrument would not be a bowing instrument anymore, which is an important factor in the design.
The bowing wheel
 Figure 1.1: Simple drawing of the bowing wheel with the string. 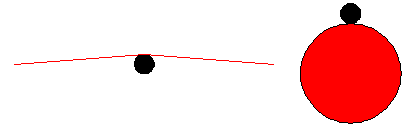 Figure 1.2: In both drawings the black dot is the cross section of the string and the bowing medium is red. Left: with a bow the bow hairs tilt slightly towards the string around the bowing point. Right: the surface of the bowing wheel tilt away from the string around the bowing point.  Figure 1.3: The bowing wheel rotating clockwise blocks the string from moving back when the string is deflected. One straightforward way to excite the string electronically is by using a “bowing wheel”, which contacts the string as shown in Figure 1.1.
As we know from practice, exciting the string using stick-slip with a bow works. It is where the notion of a good-sounding bowing sound comes from in the first place, so this should be the reference of how the bow-string interaction should be. A good way to see how well a bowing wheel can produce a sound like this is to look into how far a bowing wheel can act like a bow, and determine what exactly marks the essential difference with a bow. Finally it should be determined if this difference will pose a problem.
A set of properties of the bowing medium that influence the bow-string interaction has been assembled:
- The stiffness of the medium in z-direction
- The stiffness of the medium in y-direction
- The impulse response of the medium in z-direction
- The impulse response of the medium in y-direction
- All the surface properties of the medium (including the presence of rosin)
- The shape of the medium directly surrounding the point of contact with the string
The bow’s stiffness in z-direction can be simulated using a bowing wheel by suspending the wheel in some way in z-direction. The bow’s stiffness in y-direction, coming from the longitudal stiffness of the bow’s hairs, corresponds with the rotational stiffness of the wheel in ϕ direction. The wheel can be suspended in this direction as well, so the bow’s stiffness in y-direction can be accounted for. The impulse responses in both y- and z-directions can be simulated in the control of the rotation of the wheel and the z-translation of the wheel, respectively. The surface properties can then theoretically match those of a mat of bow hairs when a mat of bow hairs is somehow applied to the outside of the wheel. This leaves only the property of the shape of the wheel to be compensated for.
The wheel, as it is round, doesn’t have the same shape around the string as a bow. This is important because when the string transverses in y-direction (which will be the direction in which it will ideally vibrate), it keeps contact with a bow because a bow is almost straight, with the bow hairs actually tilting a bit towards the string around the bowing point, as in the left side of Figure 1.2. With a bowing wheel this is different, because it tilts away from the string around the bowing point, as shown in the right side of Figure 1.2.
This does not necessarily mean that the string loses contact with the wheel. This is because the wheel is pushed against the string with a certain force, so the string will have a static positive deflection in z-direction and is pulled down by its terminations. Because of this, as the string transverses, the string will keep contact with the bowing wheel. However, the bowing wheel is not capable of moving in y-direction, so when the string is deflected in y-direction the situation will look like Figure 1.3. In this situation the string is actually pressing harder against the wheel because of its own urge to go back to a neutral position. This causes the friction force of the wheel to increase, probably resulting in a blockage of the system.
This effect could hypothetically be prevented by the controller for the z-translation of the wheel. If the current friction force and normal force between the wheel and the string could be determined at every moment, the controller could “make sure” that these two stay at “natural” values (i.e. the same as when using a bow). This requires a constant reference for these both forces over the course of one vibration period, and a construction together with an actuator capable of following this reference with a total delay time including the sampling of the force measurements t_d that is much smaller than one vibration period, t_d≪T. This in addition with the sensors that are needed to measure the forces, makes bowing wheel a very unrealistic concept.
|