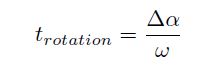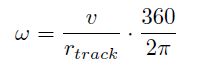Turns & Rotations
In NetLogo, it is very hard or rather impossible to visualize the proper rotations of the window
cleaning robot during its motion and subsequently end up at exactly the right position. Therefore
it was decided to not visualize the rotations, but instead, the turning movements are modeled by
letting the robot ’teleport’ from the place before to the place after the turn. The time it takes to
make a certain turn is then simply added to the time instance before the rotation. In this way, it
is still possible to model the turns and rotations of the window cleaning robot in a realistic way.
The question becomes then what will be the time that each specific turn takes? To give realistic
values for this, the characteristic rotations and turns of the window cleaning robot are studied.
In total there are six different turns or rotations which the window cleaning robot should be able
to make. They are schematically shown in the figure below.
The first turn the robot should be able to perform is a pure rotation (Figure 2.a). This motion is
very often needed during the robot’s cleaning job. To assign a time to the rotation, two parameters
should be known: the angle to which the robot is currently heading, the angle to which the robot
should head and the rotational speed of the robot when it is rotating. In reality, the robot knows
how it is oriented by means of gravity sensors and thus knows the angle to which it is currently
heading. Therefore it seems appropriate to use the angle at which the robot is
heading in NetLogo as the current angle. The time it takes to perform a pure rotation can then be
calculated by means of the following equation:
where t(rotation) is the time it takes to perform a pure rotation (s), w is the angular velocity of the robot (°/s) and Δa is the angle over which the robot should be rotated to face the upper edge of the window (°) (the angle to which the robot should head). The angular velocity of the robot is determined by using its speed and its dimensions:
where v is the speed of the window cleaning robot (m/s) and r(track) is the distance from the center
of the robot to one of the crawler tracks. The value v equals 0.1 m/s which is determined by looking
at a comparable window cleaning robot (WINDORO) while r(track) is estimated to be 0.09 m.
Another important motion of the window cleaning robot should be performed when it is for example
in the upper left corner with its cleaning section headed to the window edge. The robot has to
perform the motion that can be seen in Figure 2.b. First, it has to drive backwards to a position
where it is able to turn. Since the robot has dimensions of 25 x 25 ""cm"" the distance from the upper
edge that is needed to do a rotation can be simply calculated with use of the Pythagorean theorem:
Where s(turn) is the distance from an arbitrary edge of the window that is needed to do a rotation
(m), w is the width of the window cleaning robot (m) and h is the height of the window cleaning
robot (m). Because the robot moves over an arc, calculating the distance that it travels is very
hard analytically. Therefore a MATLAB script has been written to calculate the length of the arch
over which the robot is moving numerically. One important decision that has
been made in the script is the distance between the edge of the robot and the edge of the window
in the starting position. There needs to be a little distance between them in order to allow the
robot to turn to move away from the edge. The further the robot moves away from the edge, the more
it can turn and the faster it can get away from that edge. This means that the distance between
the edge of the window and the robot has a huge influence on the time it takes to move away from
that edge, as well as the distance traveled in the direction parallel to that edge. In the script, the
distance between the robot and edge of the window is assumed to be 5mm. Running the script
with this value yields a traveled distance s(arc,corner) of 0.33 m. Assumed in this calculation is that
after making the bend, the robot has an angle of 45° with the vertical. Subsequently, the window
cleaning robot has to do a pure rotation over 180° to make sure its cleaning pad will face the
right side of the window after the entire movement. To calculate the time that this rotation takes,
Equation 3.1 can be used again. Eventually, the robot moves again back to the left upper corner
of the window over the same arch as mentioned before.
Hence the following expression for the time of the entire movement is obtained: