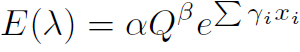PRE2016 3 Groep13: Difference between revisions
| Line 77: | Line 77: | ||
In order to say anything about the efficiency of our system we need to first look at what the possible causes of a traffic jam are. In general we can indentify three leading causes in the Netherlands for traffic jams which are: | In order to say anything about the efficiency of our system we need to first look at what the possible causes of a traffic jam are. In general we can indentify three leading causes in the Netherlands for traffic jams which are: | ||
* | * Accidents | ||
* | * Too many drivers on the road: Over Breaking | ||
* | * Road works | ||
A solution for the first cause has to be investigated more. While accidents are bound to happen as long as humans control cars (as making mistakes is common amongst humans). We do see though that accidents can be massively decreased when we decrease the amount of cars driving at a road. The busier it is the more common it is for accidents to happen. | A solution for the first cause has to be investigated more. While accidents are bound to happen as long as humans control cars (as making mistakes is common amongst humans). We do see though that accidents can be massively decreased when we decrease the amount of cars driving at a road. The busier it is the more common it is for accidents to happen. | ||
Revision as of 15:58, 30 March 2017
David Dekker - 0936100
Haico Dorenbos - 0959563
Jori van Falier - 0910959
Tim Muyrers - 0907928
Thomas Schouten - 0938927
Sten Wessel - 0941508
Introduction
Waiting for a very long time in traffic jams even when your destination is in the same city. Solving traffic problems is something that has already inspired a lot of engineers and will also inspire a lot of new engineers. “Only 10 percent of cars would have to be connected for it to work” [1] was a recent quote in an article about solving traffic jams with artificial intelligence. In our project we are also interested in solving traffic problems using artificial intelligence. This wiki page therefore will display the possibilities of self learning navigational software. Throughout the report several points of attention will be introduced, investigated and processed in the prototype navigational system. The goal of the system is to create a cooperative/inter-vehicular, high-level (for example, no traffic lights) and based on the current situation (hardly any self driving cars, not all people have navigational systems). This research is set up trying to answer the following research question:
How can the travel time be minimized while maximizing overall utility, looking at user and society, by using a Self Learning, Inter-Vehicular Cooperative Navigation System (SLIVCNS)?
Problem description
Every day in the Netherlands people go to work with their cars, and every day the same thing happens, traffic jams causing a lot of pollution and waiting time. Most of the time people are traveling a lot longer than necessary to reach their goal. This gave us the idea to create a system that will reroute this traffic through secondary roads to minimize the overall waiting time or maybe even prevent traffic jams. By doing a lot of user research we hope to create a user friendly system that will help the user and society with this problem.
The simple problem
The problem in the simplest form is as follows, there is a city A and city B, in the morning people move from A to B to go to work. There is a highway (which is the fast route) and two secondary roads. When the people move from A to B a traffic jam occurs, this causes people to wait and increases their travel time. By rerouting a part of these people to the secondary roads this traffic jam can be minimized in such a way that two things can happen, or a mix of these: 1. The traffic jam is prevented and therefore the overall travel time is a lot lower, this is hard to implement as people who had to take the secondary road have longer travel time. 2. The traffic jam has become smaller and all the people whether they take the secondary road or the highway have the same travel time. This option seems more fair but still causes the problem of people waiting in traffic jams. Which one is to be preferred has to be researched as the user is very important in this decision.
The full problem
As seen above the problem can be made very simple but also a bit unrealistic, because in the end the system has to run in the real world, where there are thousands of ways to get from A to B. Also in the real world a lot of problems arise. Traffic is very unpredictable and can come from anywhere and go anywhere. It is not simply people moving from A to B. Also a lot of people will not be using our system, we will get no information from them, but they will have impact on our system. The biggest problem is all the unknowns, a lot of things can happen on the road. For example an accident can cause a traffic jam that can not be predicted. Because of all these problems we will be using self learning software to deal with these problems. This program will try to compensate for all the unknowns.
Objectives
Minimize travel time
The main goal of the system is to minimize travel time by rerouting users, to prevent longer waiting times caused by traffic jams.
Maximize overall utility
The utility can be split in three groups.
User
- Minimize travel time, this is the main objective as mentioned above.
- Estimate arrival time by predicting traffic jams so the user knows the optimal route and best moment of departure to reach the goal location on time.
- Making the system fair for all users. This will require user research in finding the fairest solution.
- Taking the privacy of the user into account by doing user research.
Society
- Traffic jam prevention to minimize unnecessary pollution, by rerouting to minimize unnecessary waiting time.
- Minimize disturbance by rerouting through less populated locations.
Enterprises
- Creating a system that is better than the present navigation systems, so potential users will be interested in buying this system.
State of the Art
There are a lot of different navigation devices available currently. The most simple one is only able to tell you the shortest route. A small upgrade also allows the user to exclude certain routes, like toll roads and tunnels. These often also give a choice for the user to either take a fastest (time) or shortest (distance) route. Some devices also allow traffic information incorporation which ask you to reroute if there is a traffic jam. When combining such a navigation system with a self driving car it is also possible to make the decision automatically. These all however respond to a situation instead trying to avoid certain situations.
Improvement over state of the art
To improve the state of the art it is important to know what the implications are of the current system. These systems will reroute users as soon as there is a faster route available and thus will distribute traffic equally over the roads available, which may seem like the optimal situation. A self learning system however should have more roads available, since it can predict traffic jams that haven't even happened yet. It can reroute the user many kilometers before the actual traffic jam and thus prevent new traffic jams in reroute roads.
Approach
The goal of the research is to improve the current traffic situation. This can only be considered an improvement when the changes do not diminish the overall utility. This means that within the navigation system the user as well as the society have to play an important role. As the time window is quite a tight one this research will be conducted simultaneously. The group of researchers will be split where four members of the team will work on making the self learning navigation work. The remaining two members will focus on the users and society. By frequent interaction, the team will be able to create a working navigational system in which the user and society will be strongly embedded. This also allows the prototype to be as representable as possible.
The completion of the program will also include a visual simulation which allows all team members as well as external personnel to use and understand the way the system operates, and what conclusions it provides.
User and Society
People behave differently when wearing something to hide their identity[2]. This also happens in a car. People are not directly visible and thus act more selfish. As long as people are driving their car (instead of autonomous), we can investigate further if/how we want to incorporate this.
Furthermore our navigation idea will request people to drive different roads, which at points will probably make them lose time on their journey. When looking at literature we find something called: “risk aversion”[3] [4]. Risk aversion is a human trait where someone would avoid taking a favorable bet (overall travel time decrease) when it means they can directly lose out (more travel time) [5].
What is a traffic jam
In order to say anything about the efficiency of our system we need to first look at what the possible causes of a traffic jam are. In general we can indentify three leading causes in the Netherlands for traffic jams which are:
- Accidents
- Too many drivers on the road: Over Breaking
- Road works
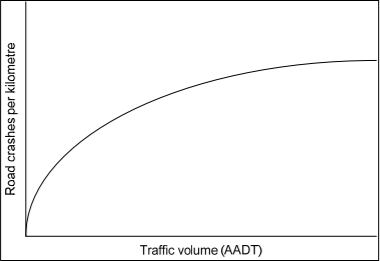
A solution for the first cause has to be investigated more. While accidents are bound to happen as long as humans control cars (as making mistakes is common amongst humans). We do see though that accidents can be massively decreased when we decrease the amount of cars driving at a road. The busier it is the more common it is for accidents to happen. A study performed in 2010 [6] found a relation between business on roads and accidents.
E(λ) being the estimated number of crashes, Q is the measurement for traffic volume, xi is the risk factor, γi is the corresponding coefficient to the riskfactor and finally β is the effect of the volume of traffic on crashes.
Too many drivers on the road also causes direct traffic jams through over breaking. When a car in front breakers the one after it breaks too but a little harder thus going a little slower. The person driving behind this person does the same and thus it will eventually reach a standstill.
Road works can’t really be avoided. But if the system is connected to a database, it should be able to take this into account.
While reaction systems are able to deal with most of these issues, it cannot prevent accidents from happening. While a self learning system should be able to.
So to make sure the navigational system works in society you have to give it a certain goal of not exceeding a density of cars on the highways. For testing purposes you could look at a particular road and figure out the relation between accidents and car density. More research is needed for an accurate relation between traffic density and accidents. As the study from Kirsten Duivenvoorden [7] explains current research is mostly focussed on geometric variables, meaning the median and width of roads, the presence of turning lanes and presence of traffic lights and traffic speed. The reason for this is that in the past the volume could not be changed, and thus this wasn't the aim of researchers. With this new technology this can however be influenced and thus more research would be benicial.
User research
Already done research
We base already done research on a questionnaire about navigation systems done by “Kennisinstituut voor Mobiliteitsbeleid (KiM)” from the ministry of infrastructure and milieu. [ ] This questionnaire has 3.924 respondents from car drivers of the “Mobiliteitspanel Nederland (MPN)”.
Current navigation system are rarely bought because of traffic information. Most of the information comes from the internet and the radio and during the travel also information panels above the road (DRIPs). From the questions follows that easy in use and quality of information are important reason for people not to use the navigation system solely for traffic information. That is where our navigation system can make the difference. By making an easy to use system with reliable information, we hope our system will be of interest for the user.
Navigation systems are mostly used for non-frequent or long distant travels. The system is also used for points of interest. The most used points of interest are parking lot (75%), gas stations (49%) and places of entertainment (38%). Furthermore the system is used to avoid toll roads and ferries. All these options might be interesting to implement in our system.
Route taking
Something else of important follows from the research done here. Most users will choose for the fastest route (60-70%), also the default setting is used a lot which is the fastest route in most cases. Also a relatively large amount of users deviate from the route given by their navigation system, mostly because they know a better route, heard or seen a traffic jam, or because of road works. Because our system will only work when everyone using the system, follows the system, it might be very important to inform the user that our system has noticed these traffic jams and road works, and that we can proof that our system can find the most optimal route for the user.
Our user research
To make sure all user preferences are taken into account a user research is conducted, focusing on the key aspects which should provide a strong basis for the product to be released to the public. The aim of the research, and thus leading factors into choosing the approach, is to gain as much information about as many different drivers as possible. Since the aspects of the research are predetermined, the best research method available is a questionnaire. Google Drive is used to host the questionnaire, because it has all features (sort of questions/ set-up) required for this research.
The link below will bring you to the questionnaire*:
https://docs.google.com/forms/d/e/1FAIpQLScDPnmNoF6QXpMX930HC-V1ydxndn6kBt-_NZO-LiEaaBGuWA/viewform
- Please note that by choosing certain answers it is possible that the questionaire forwards you and thus skipping certain sections. In order to see the full questionaire, make sure to not answer the questions and just go on to the next section.
The questionnaire is divided in several sections. Just like any research the questionnaire begins with a brief introduction of our idea followed by asking the participants permission to use the data they provide through an inform consent form. In all following sections the key issues are presented to possible users. To make sure everyone recieving the questionaire will be able to understand and participate an English and Dutch version is available.
The target group contains all drivers, both frequent and non frequent drivers. While the system is designed for non selfdriving cars it would also work on autonomous cars. The system will first be tested and deployed in The Netherlands and thus this is also the target group for distributing the questionaire.
Section 1: Introduction questions
The system investigated is a navigational system. Thus it is important that the participants are actual drivers, and thus the introduction asks the participants this question. It also briefly looks into the preferences a car owner has.
Section 2: Willingness to follow the system
A navigation system could work very well, but in the current situation it is still the users controlling the car. Since SLIVCS is designed to be applicable into society at this moment it thus is dependent on the willingness of the user to follow its instructions. If an user would stray from the path the system proposes often the system would no longer work. This section proposes several situations to the participant and asks the user whether or not he would follow the system (thus believing and whatever the system proposes it should still be faster then not listening to the system).
Section 3: Fairness
The system can decrease travel time and traffic jams in several ways. The participants are presented with this way in a honest way. This means that we do present options where a user of the system is always equal or worse of to a person not using SLIVCNS. This sections is designed to get a better understanding of the target group, and to give a better insight into the goal our system should aim for.
Section 4: Privacy
The current state of the world means that almost all information gets shared [8]. This however does not mean that all users all necessarily willing to share all information. Since our system needs to know certain things about users it is important to know that people do not mind sharing this information (anonymously). We ask the participants if they would be willing to share their current location as well as their destination. If the participant is willing to share this he/she is taking to the next section with follow-up questions. If the participant is not willing to share this information he is taken to the final stage of the questionnaire.
Section 5: System interaction
In this section the participants are asked to think about the idea of SLIVCNS, and how they would see such a system fit in their daily lives. It contains three subsections. The first subsection asks the participants what inputs they would like to have on the system. There are six predetermined options, like what type of roads, should the system take pollution into account etc. It is also possible to write your own input, if this is not present in the existing questions. The second question makes the participant think about how they would like to communicate with the system. As explained in Chapter %%%%%%%% it is important that the system knows when a user wants to travel from a to b. This means that a user would need to interact with the system quite frequently, which means that this interaction should be easy. Possible communications are for example a mobile app, an online website or a custom made interface. Once again the questionnaire provides room for a written answer. The final subsection is regarding the route planning of possible users. For the system to work optimally it is beneficial to know way in advance when users are going to drive. This section asks of different occasions (different destinations) the time a user would be able/willing to provide the system with its travel plans before departing.
Section 6: Finalizing questions
This section is focused on the aim of the navigational system. In this section the participants are asked about possible approaches the system could take regarding traffic/travel time distribution.
A participant is free to not answer a question if he/she does not want to answer, without having to provide an reason. All information helps towards optimizing SLIVCS for the user, and thus there are no mandatory questions (excluding accepting the inform consent form).
Outcome user research
Outcomes summed up:
- 63 participants
- Representable participants (drivers)
- No clear answer to environmental factors that should be taken into account
- The idea is well recieved with up to 95% of the participants showing interrest in the product
- 72.4 % of all instructions by the navigation system will be followed (clear distinction between routing via the fastest way (highway) vs sending the users on secondairy roads)
- Point based system or reward for driving longer routes is preferred amongst the participants
- 82.5% and 79.3% of all participants indicate they are willing to share their current location and destination
- Important to know how the navigation system will be limited by allowing users to choose or decline certain road types
- Mobile app is preferred device to interact with the navigation system
- Over 75% of participants are willing to plan their travels ahead of time and inform the navigation system of said plans.
Per section of the questionnaire the general outcomes will be explained and what this means for our design.
In total 63 people participated in this study (and it is still open for responses until 7th of April). Seven people responded to the English version and fifty-six filled in the English version. Out of the 63 participants one person was not qualified to participate and thus only declined the inform consent.
The introduction questions focused on introducing the product and for us the investigators to get familiar with the target group. Approximately 74% of the participants indicated to use a car on a regular basis. After a short introduction 95% is interested in the product. When the participant is asked what environmental nuisances the system should take into account a wide array of answer are given. The possible answers “No pollution nor noise disturbance”, “pollution”, “noise disturbance”, “both pollution and noise disturbance” got 25.8% 26.4% 9.9% and 37.9% respectively.
So what does this mean. To start it means that the target group intended for the research in reached. The majority does regularly drive a car, and thus are potential users of our system. With 95% of the participants being interested in the system shows that the potential for a successful device is high. It also means that if developed well it would gain a large market share and thus function well through inter device communication. As for environmental nuisances it’s hard to say how the device would be optimized at this point since the answers are divided amongst all four categories.
The second question category tests whether or not participants are willing to follow the system in four situations. Over all four categories an average of 72.4% was willing to follow the system. There are however differences between categories. Participants indicated they were 98.5% willing to follow the system if a traffic jam was already on their route, while only 50% would follow the system if it sends you on a secondary road with the aim of avoiding a traffic jam for other drivers. While (as we will see later in the questionnaire results) the system would be optimized to get the optimal drive time for all drivers it would be important for users to understand and believe the effectivity of the system. While a willingness of 72.4% is a strong basis for the system the function well, a higher percentage would increase its effectivity. The next section is about how our system should function to decrease travel time. There are four proposed approaches and ideally one would be the best. The preferred options are a point based system that will sent you on a longer route, but sends you on a shorter route the next time. Also the idea of a reward (not defined) sounds appealing to a large part of the participants with both sections respectively scoring 81.9% and 73.8% on Very good or Good in comparison with the sum of all participants. For the design of the system this would mean that there is more room for the designers to reroute cars to avoid traffic jams completely. It does however also mean that it is important to include regulatory bodies like the government into the process to discuss possible rewards (if this choice is made).
As explained earlier the system has a couple of areas which require users of the system to facilitate the system certain information to function optimally. The section privacy investigates if users are willing to provide general navigation information for the system to use and process. As expected from the current situation of navigation systems the hypothesis of users willing to provide the system with some of their information is confirmed. Respectively 82.5% and 79.3% of all participants indicate they are willing to share their current location and destination.
The next section is aimed at making the product more appealing to users. Here several inputs are proposed which will decrease the system performance. However if this makes the product reach more people this fall in performance will most likely be compensated by the extra information the system is able to receive from more users. 36% of the participants would like to see an option to tell the system if they are in a hurry or not. A design choice is made that only options which more than half of the participants would love to see in the system are considered (because previously mentioned reasons). Approximately 71.4% of the participants however are interested in being able to tell the systems what roads they like to take or avoid. This means that this option should be more investigated, since the system should have a large degree of freedom in deciding which route to take. Having users choose their own paths defeats the purpose of the system.
[[[[[[[[[Toevoegen nuisance/noise polution]]]]]]]]]]
Making system interaction easier is a strong aim in future planning of travels. For this a section of the questionnaire is design specifically to understand how participants/drivers would like to do this. The aim is to design one maximally two devices to keep the costs low and the usability high. Only one device is liked a lot by the participants which is the mobile app. Since the app is an excellent way to also inform the device of you travel plans over a large distance it would be able to provide pre planned travel trips. For the end product this is a good outcome.
The next section of the questionnaire continued of the planning and information exchange between user and device before departure. The most important input is regard work travel as this is the most frequent reason for travel [9] .
As you can see in the graph above on any occasion more than 75% is willing to inform the system ahead of time with the users intentions. This is a positive outcome, since future route planning could be incorporated in the system. Besides self-learning traffic patterns it can now also use data provided by users to make conclusions about the traffic situation.
Finally like in the beginning the participants are once again presented with several possible goals of the system and if they would use the system accordingly.
In the section above this we explained the conclusions drawn from the quantitative questions. However participants were also able to give qualitative (open questions) answers. The main findings from this will be explained below:
Future user research
Improvement over the done research
In the research we have done, a lot of things could not be specified. For example the amount of increase in travel time in order to decrease pollution and noise disturbance is not known to us. Same goes for the increase in travel time to decrease traffic jams for other users. In this stage of the development these things can not be specified. The questions we asked were more for a general understanding of the user needs, and help us choose the right direction for the system. Once the system is further developed more specific questions can be asked, as a lot more of the system is known. The research we have done has been on a selective group that is not a good representation of the population. Furthermore the amount of reactions is only a very small fraction of the population, in order to get reliable results the questionnaire should be send to more users. This will make the representation of the population more accurate and maybe some compensations have to be made, because not every type of user is willing to fill in a questionnaire.
Extra research
The system will require an interface that has to be developed. This interface has to be user friendly, by being easy to use and understandable for all users. This is why during the development of this interface a lot of user research has to be done to create a user friendly interface. This is not the focus of this project, but has to be done if the system would be developed further. Other research like society research, is also of great importance in the development of this system and if the development is nearing its end, research about bringing the system on the market has to be done. For this project where we are in the early stages of development these things can not be researched by us, because we do not know enough about the system.
Low Level Implementation Ideas
Brick Algorithm
Introduction
We start by introducing a very easy model for our problem. It is not very expanded and therefore the model doesn’t really look like what will happen in the reality. In this model we only take into account the waiting time of driver (so no privacy, pollution, etcetera is taken into account ). Furthermore in this model we look at one part of the day: the morning rush and we will assume that everyone travels to the same destination. Our model is completely static and ironically it doesn’t take time into account. Moreover we assume that everyone uses our clever navigation system and that everyone is obedient to our clever navigation system and therefore they will always follow their directions.
Situation Representation
We will represent the current situation as a graph with vertices and edges, thus it will look like this:

The vertex that is two times circled is the destination, which means that the drivers from cities B, C and D have to go to this location (we don’t take drivers from city A into account, because they already arrived at their goal). The edges are driveways with a specific direction. So for each road there are two edges, because you can take the driveway forward or the driveway backward (for destination A however there are none driveway backwards, because if you are at destination A then you don’t have to drive back). Every driveway in this graph is indicated with a number and every city is indicated with a letter.
Data about roads and cities
We will assume that 30.000 people live in city B who all need to go to A. We will furthermore assume that 20.000 people live in city C, who all need to go to city A. Moreover we will assume that 10.000 people live in city D, who all need to go to city A. Last of all we will assume that the waiting time for each road is determined by a simple linear function: ax + b, where x is the amount of driver over a driveway (we will see later how x is determined), a is the capacity constant of the road (if it is lower then it can handle more drivers) and b is the constant, which indicated how much time drivers take minimal by taken a driveway. The result of this function is the amount of minutes that drivers have to wait before arriving at the new node. Now we have some more information about the roads:
- Roads 1 and 3 are huge highways (they can handle a lot of drivers), therefore they have the function 0.00025x + 15 (you need at least 15 minutes to drive over that certain road)
- Roads 2, 4, 5, 6 and 7 are little, short roads (In dutch: N-wegen) (and they can only handle a small amount of drivers) and these roads have the function 0.0005x + 5 (you need at least 5 minutes to driver over that certain road).
- Roads 8 en 9 are small, very short roads (you are soon at the new node by using this vertex) and have the function 0.0005x + 3 (you take at least 3 minutes to drive over that certain road).
How to determine x (amount of drivers over a certain road)
Driver can take different roads. Of course this will influence the value x. In this algorithm the value of x will start at 0, because at the start of our algorithm. Suppose we have some driver that live in city C, which drives over the driveways 6, 5 and 1 (in this order) and finally arrives at his destination A. If this happens then the x value for driveways 6, 5 and 1 is incremented by 1. Therefore the x value for driveways 6, 5 and 1 is now equal to 1. This is executed for all drivers, they keep driving over the driveways until they reach their final destination A and for every driveway we will increase the amount x by one if a new driver uses this driveway.
Comparing Solutions
Each way of driving must be comparable with each other way of driving (it must be a total order, so you must be able to say whether a < b, a > b or a = b). A value (cost value) is assigned to every solution (route drivers might take). The cost value that we use in our case is the sum of all waiting times for each driveway multiplied with the amount of drivers that take that certain road. So for example if 10.000 people have driven over road 1 and they have waited 17,5 minutes then the cost value for this road is 175.000, this will be summed with the cost values of all roads and then we will have our final cost value. A solution is better than another solution if it has a lower final cost value. Therefore our goal is to minimize the final cost value.
How will the drivers behave in optimal case?
That is something this artificial algorithm will determine (by assuming everyone will follow our clever navigation system). The main idea is that we will use a distribution table, where every driveway gets a certain value (tried by our artificial algorithm could be for example a gradient optimizer or a genetic algorithm). But how do drivers behave when all values are assigned. Suppose for example that driveway 1 gets a value of 20, driveway 4 gets a value of 40 and driveway 9 gets a value of 70 (those are all outgoing driveway from B) then this algorithm will say that (20/(20+40+70)) = (20/130) relative amount of all drivers from city B will take driveway 1, moreover (40/130) will take driveway 4 and last of (70/130) will take driveway 9. This will be done at the start of this algorithm for every city. Of course after this is done, not everyone has arrived at destination A. So we have to do this again and use the same distribution table. Hence city B has after the first “driving” round a new amount of drivers, which is equal to the amount of driver that went from city D to city B (by using driveway 5) added with the amount of drivers that went from city C to city B by using driveway 8. After this we will get a new “driving” round. This script will continue until everyone arrives at destination A.
What will happen if none or a few drivers to go city A?
We will limit our script till 10 “driving” rounds for example (you can take a different number than 10). If after 10 “driving” rounds not everyone has arrived at destination A then it will get a very high cost value (and therefore this is automatically a very bad solution, worse than solutions in which all drivers arrive at destination A). Our idea was for example to say that this value is equal to (Float_MaxValue) * (amount_drivers_at_start - amount_drivers_reached_destination) / (amount_drivers_at_start). This cost value has to be definitely higher than a cost value of a solution for which it is possible for everyone to arrive within 10 “driving” to destination A. If we define our cost value this way then a solution for which 10 “driving” rounds is too less to for everyone to get to their destination is worse than a solution in which everyone get to their destination in 10 “driving” rounds.
Advantages
- It is a very simple model, because it doesn’t need Neural Networks or other complex ways to find the solution. A gradient solver or genetic algorithm is enough to solve this problem.
- It can be easily expanded to multiple goals, where from each city they need to go to different nodes. Also for different times it can be used. Thus it will always find the best solution for every case, so it is complete and optimal.
Disadvantages
- Assumptions were made which are not very logical (waiting time is a linear function is not a very good assumption for example, likewise assuming that everyone will use our clever navigation system).
- For larger areas this algorithm will take a lot of time. Especially because this algorithm need to determine driveways * destinations * different_parts_of_the_day amount of constant. If you look for example at an area Germany and the Netherland then there is a huge amount of driveways and a huge amount of destinations. Hence you will have to determine a lot of constants.
- Because of the reason before this algorithm will also take a lot of memory for larger areas.
Matrix Algorithm (A first attempt at an implementation)
This is a way of optimizing to a very specific problem, with a given situation. It optimizes for that situation, so it will never be a real, general solution. It works by changing the input to something better, instead of learning how to convert any input to a certain solution.
Please remember that the problem solved here is mainly to get a feel for both the programming language and the type of problem. We know this problem is so simple you could easily solve it by other means, with much less effort, but that is a good way of checking our own results.
We assume there are two cities, A and B, and two roads from A to B. We assume cars leave in driving rounds, so in each round there is a certain amount of cars on the road. For example, a typical distribution of cars over one road would be [12, 3] which means that the first round 12 cars leave city A, and the second round 3 cars do so.
Of each road we know exactly how much time a car needs to travel the road given how much cars are on the road in total. This is a function which we will call the travel time function. We assume here it is of the form max(a * cars - b, min_travel_time), which means that up to a certain amount of cars on the road the travel time equals the minimum travel time needed to traverse the road, and above that the travel time increases linearly. The latter case is of course meant to signify a traffic jam.
One road is a highway, and the other road a secondary road which means that on the secondary road the minimal travel time is larger, a traffic jam occurs with less cars, and increases more per extra car. This is easily extendable with more roads, but for every road you would have to know this travel time function.
So for two roads together we have again a distribution matrix, for example [[8, 3], [3, 1]]. The idea is that we predetermine the amount of driving rounds, because changing the size of this matrix while optimizing is a bit of a problem still. (As a sidenote, in real life you would probably want to limit this because of user preferences anyway)
Optimizing the distribution matrix
We calculate the cost (travel time) of a certain distribution matrix by adding up the travel times of all the cars. This is the value that is going to be minimized. For the cars leaving the first round, the travel time for each car is given by the travel time function. For the cars in the second round, the same holds but we add the time that they had to wait while the first round was driving. We continue this for how many rounds there are. Then, if there are still cars left after all the rounds, we assume all these cars depart in the last round.
The program optimizes this matrix by minimizing the costs. Therefore, if there are sufficiently many rounds, no cars will be left behind, because if the number of rounds goes to infinity the cost of leaving cars behind will go to infinity as well.
The program
The program, written in Python with Tensorflow, has as input the matrix initialized with some values which should not matter too much. It then uses a Gradient Descent Optimizer to minimize the cost. The optimizer is run for a certain amount of steps with a certain learning rate, and then it outputs the optimized distribution matrix.
Drawbacks of this approach
- We have to predetermine the amount of driving rounds.
- We have to know for each road the travel time function.
- This generalizes and scales badly, because the matrix will get very large, and you need a matrix for every possible trajectory between two cities.
Problems with the current program
- It is very slow.
- When normalizing the distribution matrix values to a fraction of the total amount of cars instead, it should be more stable because it does not have to change values to whatever big amount of cars there may be so the learning rate can be smaller, but instead the results get very unstable.
- Currently when on the first round each cars take for example ten minutes to clear the road, the next round can depart after one minute if that is the minimal travel time. Changing this leads to unstable behaviour.
ILDB(+) Algorithm
Introduction
ILDB Algorithm stands for “Iterating Limited Distance Brick Algorithm”. This algorithm is an expanded version of the “Brick Algorithm”. Therefore it is really important to have read the “Brick Algorithm” and understand how it works. This algorithm is an improve of the “Brick Algorithm” because it also work for a more larger scale. The idea of this algorithm is based on that traffic jams only occur at local scale, which means that if a lot of traffic has to go to Eindhoven then the traffic jams occur close to Eindhoven.
Situation Representation
We are trying again to see the problem as a graph with nodes and vertices, likewise the “Brick Algorithm”. However this time the graph is more complex (to illustrate the difference between the “Brick Algorithm” and this algorithm):
In this example A, G and J are goals. And to make the situation less complex we will assume that cities with subscript A have 2000 humans that need to go to A. If a city doesn’t have subscript A then 200 humans need to go to A from that city. For subscript G and J the same holds. Furthermore we assume that every black road has 1 lane and has a minimal time of 10 minutes. Every orange road has 2 lanes and has a minimal time of 20 minutes. And every green road has 3 lanes and has a minimal time of 30 minutes. Then we also have red road, which has a minimal time of 15 minutes and has 1 lane.
Calculation Waiting Time
The calculation of the waiting time for roads is the same as the Auction House algorithm.
How does the algorithm works?
In the “Bricks Algorithm” you have different driving rounds. In this algorithm you get some new type of round called iteration round. We first take a look at a certain radius from every goal by only looking at minimal time and we take 30 minutes for example. So every node that is in t minutes of a goal is taken into account. We take t is 30 minutes in this example and you might notice that every city that has a subscript of that certain goal is within 30 minutes of that goal. Then we start with the first iteration round:
First iteration round
In the first iteration round you will use the “Brick Algorithm” for every goal separately and for everyone that has to go to his goal and is within t minimal waiting time from its goal. You will discard every node in this example that is further than t time from its goal and every road that goes to a discarded node or comes from a discarded node is also discarded. So in this example you will use the “Brick Algorithm” for three zones with subscript: A, G and J (note that zones doesn’t have to be disjunctive) and you will found the optimal solution for these zones. After that (same iteration round) you will take back the discarded nodes and vertices and take a look at humans that will travel to a goal and are outside of that zone (so for example someone from a city that hasn’t got subscript A wants to travel to A). In this case you will use the shortest path algorithm to that certain zone taken into account the new waiting time due to the traffic jams that drivers within a zone have created. If travelers from outside the zone enter the zone with their shortest path algorithm, they will use the “Brick Algorithm” to get to their destination.
Other iteration rounds
The second iteration round is executed after the first iteration round is executed for every goal zone and the second iteration round will check where the drivers from outside the zone have entered the zone in the first iteration round and will take them into account as new inhabitants of that node that have to go to that certain goal for the “Brick Algorithm”. So suppose 500 outsiders have entered zone J by going to H, then in the “Brick Algorithm” drivers that have to go from H to J is increased by 500. After this a third iteration round is executed and will take the results of the second iteration round into account etc. This iteration is stopped after u iteration rounds have passed where we will determine u based on the calculation time of this algorithm.
What if two goals are close to each other?
This algorithm calculate separately for each goal what the optimal local solution is, however if two goals are close to each other then it will not take the other goal into account, which might be bad. Therefore you might say that when you calculate the local solution for a certain goal that you also take other goals within a radius of 2*t into account, so you will use the “Brick Algorithm” for multiple goals at the same time. Then you discard the result of the other goals and you will use only the result of the goal that you were calculating. This algorithm will be called “ILDB+ Algorithm”.
Defense of Assumption
The ILDB Algorithm is based on the assumption that traffic jams for traffic going to a certain location only occur close to that location. This assumption is very logical, because if for example there is some event going in Amsterdam and a lot of drivers from Berlin go to Amsterdam then no traffic jam will occur in Germany because of the drivers that will go to Amsterdam (traffic jams in Germany might happen, but they have a different cause).
Advantages
- It can also solve the problem for larger problems more efficiently than the “Brick Algorithm”.
- It needs less memory than the “Brick Algorithm” to solve the problem.
- It doesn’t need Neural Networks or other complex ways to find the solution. A gradient solver or genetic algorithm is enough to solve this problem.
Disadvantages
- It is harder to see if this algorithm is complete and always find the most optimal solution than for the “Brick Algorithm”, because a lot of path distributions are discarded in this solution.
- If the assumption that traffic jams going to a certain location only occur close to that location is a very wrong assumption, then this algorithm doesn’t work (if it is partially true then this algorithm might still work).
- This algorithm is more complex than the “Brick Algorithm” and therefore harder to understand and implement.
- In this algorithm we must determine ourselves how much iteration rounds are needed and what the value for t is.
Results
The ILDB algorithm has been implemented in Java and has been tested. A bit changes were made to make this algorithm run more faster and make the code less complex to make and to understand. These changes were:
- Set the amount of iteration rounds to 1 instead of some other constant higher than 1.
- Only take local traffic into account when training. So traffic that is within radius t of that goal and need to go to that goal is taken into account. Therefore traffic that needs to go to the same goal that are outside radius t and traffic that needs to a different goal is not taken into account when training (but is used afterwards to show the total driving time for all drivers given a certain solution).
- The normal part of this algorithm is implemented, so the + part is not implemented.
- Random graphs were used with one goal to test the efficiency of this algorithm.
The time complexity of this algorithm to train is constant time compared to the amount of nodes and vertices in the graph that are not goals (because the distance in which the Brick Algorithm is runned is limited). You can also see why this algorithm is very efficient compared to other algorithms. For a graph with 120 nodes and 180 vertices and 1 goal it takes about 6 minutes and 29 seconds to run. It is a bit harder in this case to see why the solution the algorithm returns is the best one. However you can see that for a certain radius t the total driving time of all traffic doesn’t decrease much if you continue with increasing it and strange enough the total driving time increases a bit sometime for higher radius t, because with a higher radius t you have a lot more distribution constants that have to be determined for different roads and therefore you have more local minima in which this algorithm get stuck. All considered we have decided to not use this algorithm for our final implementation. This might sound strange because other algorithms have a higher time complexity than constant time, however the constant time in this algorithm is very high and therefore because we only use small graphs in our final implementation we don’t use this algorithm for our final implementation.
High Level Implementation Ideas
Auction House Algorithm
Introduction
Before reading and understanding this algorithm you have to read and understand the Brick algorithm. This is the first algorithm that uses a Neural Network, therefore this algorithm might be hard to understand and difficult to read. So let's start with the algorithm, we called this algorithm “Auction House Algorithm” because it is a little bit comparable with an auction. Every road that you might take to get to your final destination, will be auctioned to everyone that might as well take the same road. An auction has some similarities to this algorithm. In an auction you will bid on something that has some value for you, but when the bid of someone is much higher than you wanted to offer, then it might be a good idea to stop with bidding any higher, because it is most likely the case that the item that is being auctioned is more valuable for the other than for you. Something similar happens in this algorithm, we will take a look at a certain road and check how much it is worth for a certain city. This value will be compared with the value of this road for other cities. This might sound very complex, therefore we will start by introducing a definition list:
Definition List
- Route: A set of roads that will take you from your start location to your destination.
- In Advance Best: A route is in advance best if it is the shortest route to your destination, without taking traffic jams and other things that might happen in the future into account. When we talk about m in advance best routes then we talk about the best m in advance routes (so the in advance best route, the second in advance best route, etcetera). m is in this case some constant, which will will determine.
- Capacity: The maximal amount of cars that can take a certain road each hour.
- Claiming: If in the m in advance best routes from a city to a destination, you will take a certain road then that city is claiming that road.
- Neural: Neural(arg1, arg2, …, arg n) is the output of a Neural Network with n input arguments.
Situation Representation
The situation representation is the same as the Brick Algorithm:

Data about roads and cities
The data about the cities will stay the same, however the data about the roads will change. We will assume that there is a maximum capacity for every road. And this is the maximum capacity for these kind of roads:[10]
- 1 Lane: 1750 vehicles per hour
- 2 Lanes: 4200 vehicles per hour
We will define that roads 1 and 3 have 2 lanes. All the other roads only have 1 lane. The minimal driving time will stay the same:
- Roads 1 and 3 have a minimal driving time of 15 minutes.
- Roads 8 and 9 have a minimal driving time of 3 minutes.
- All other roads have a minimal driving time of 5 minutes.
The driving/waiting time of a road is easily determined. We will assume that the spits (Dutch word for the moment that everyone needs to go to work etcetera) will have a duration of 2 hours. And that when x amount of people in the spits need to go over a certain road, then the demand for that road each hour is x / 2. When x / 2 is smaller than the maximal capacity or equal, the the driving/waiting time is equal to the minimal driving time of that road. When x / 2 is larger the maximal capacity of that road then the driving/waiting time is determined by: (x * minimal driving time) / (maximum capacity * 2)
Determine the value of a road
From every start location, destination combination we will take the m in advance best routes. For every start location, destination combination you can determine what the value is for a certain road which will be claimed by that start location, destination combination. This will be done by assuming that the road might not be taken to go to your destination. To determine that value we will first define some other values:
- Shortest path with road (a): The total driving time that someone needs to go from its location to their destination with the in advance best route without taking traffic jams, etcetera into account.
- Shortest path without road (b): The total driving time that someone needs to go from its location to their destination without taking traffic jams, etcetera into account, using the in advance best route, given that the route might not use this road. (If there is no possible route anymore to the destination then this value is equal to infinity. In the case you use a limit value, then this value is equal to the limit value instead of infinity.)
- Own total time with road (c): The total sum of the times of different routes that someone from a city needs when using the m in advance best routes without taking traffic jams, etcetera into account.
- Own total time without road (d): The total sum of the times of different routes that someone from a city needs when using the m in advance best routes without taking traffic jams, etcetera into account. Also given that the m in advance best routes might not use this road.
- How much other claims (e): How much other start location/destination combinations make a claim on this road.
- Sum shortest path others with road (f): The total sum of the shortest path with road for other start location/destination combinations (including other destinations from the same city).
- Sum shortest path others without road (g): The total sum of the shortest path without road for other start location/destination combinations.
- Sum total time others with road (h): The total sum of the own total time with road for other start location/destination combinations.
- Sum total time others without road (i): The total sum of the own total time without road for other start location/destination combinations.
- How much people claim the road (j): The total sum of all drivers that claim this road.
- Capacity of a road (k): The maximal capacity of a road.
We will define: l = Neural(a, b, c, d, e, f, g, h, i, j, k). l is probably a value between 0 and 1 (because it is the output of a Neural Network). The value of this road is equal to: e^(tan(π∙(l-0.5)))
Why such complex function?
Because this function has nice properties:
- When l goes to 0 then this function converges to 0.
- When l goes to 1 then this function diverges to infinity.
- e^(tan(π∙(a-0.5))) ∙e^(tan(π∙(b-0.5))) = 1 if a = 0.5 – x and b = 0.5 + x (so opposites neutralize each other)
- e^(tan (π∙(l-0.5))) = 1 if l = 0.5
How does the algorithm furthermore work?
For each start location/destination combination a value is assigned the m in advance routes. This value is calculated by multiplying all values of the roads which this route takes. This way you get a r1 value for the in advance best route, r2 for the second in advance best route, etc. Moreover you will distribute different citizens in a city based on their destination over different routes. Route i will take ri / (r1 + … + rm) relative amount of the drivers from the city that need to go to that destination.
Why not an unlimited m?
A good question is why not unlimit m in taking the in advance best m routes into account, because taking every route into account is better than taking not every route into account. This is done to limit the running time of our algorithm. For example if you take a look at all possible routes from Berlin to Amsterdam then it takes ages for our program to find all possible routes from Berlin to Amsterdam, because our script then also takes routes into account that go through Italy. Therefore you must limit the amount of routes that is taken into account by a certain constant m, because it is not very likely that the best path from Berlin to Amsterdam goes through Italy, not even when you try to prevent traffic jams. Thus logically the route you must take to prevent traffic jams and to go to your destination is within the in advance best m routes. This m doesn’t have to be an independent constant, but could for example also be dependent on the distance between your location and your destination. However we are not sure how to do this. So we take an independent m that is large enough to get the best solution, but small enough to get a good running time.
Further thoughts on the problem
Solving the problem in a ‘classical’ reinforcement learning way, would be defining actions like delaying cars (sending them away later) or sending cars over different roads, and then define a network which attaches probabilities to these actions. Then you train it with quite some situations, and then it develops a policy of probabilities of when to send cars. Basically it learns what to do with all the cars that want to leave.
We want to use the NEAT algorithm, in the form of the NEAT-Python library. In very short terms, this algorithm evoluates a neural network with an evolutionary algorithm, and therefore you do not have to design such a neural network yourself.
We want to find out how we can solve this reinforcement learning problem with NEAT-Python.
NEAT Algorithm
The reinforcement learning approach enables us to not only get a solution to the problem of rerouting traffic, but also gives us part of the solution strategy: the weights of the neural network connections. Thus, we do not have to determine the optimal network weights in the network beforehand. For solving the traffic rerouting problem, this is essential. Because of the many input factors involved for which the effects and their influence thereon are unknown or uncertain, we cannot possible construct a good model for this system.
To apply reinforcement learning, we need a neural network to manipulate the weights for to optimize its performance. Thus, we need to construct the topology of the network beforehand. Conducting a study in different variants of neural network topologies gives a lot of options to choose from, each applicable for a specific problem domain. See for instance The Neural Network Zoo by the Asimov Institute[11] for an extensive list of possibilities. Determining a suitable topology for our problem is challenging, because of the unknown underlying structure and the scope of relevant factors. However, if it is possible to evolve network weights, why would it not be possible to evolve network topology? We turn to the NEAT algorithm, short for NeuroEvolution of Augmenting Topologies, specifically designed to do that. It was originally developed Ken Stanley in 2002[12] and modified and extended over the last couple of years.
Double Pole Balancing
To understand how this works, we introduce a famously investigated problem in the area of artificial intelligence: the double pole balancing problem. This problem has been widely used as a measure for the performance of an artificial intelligent system. It involves a cart moving in a bounded 1-dimensional space (either to the left or right) on which two poles of a different length are fixed at one end at the same point on the cart (see figure).
In the initial position, the poles stand upright and the cart has a nonzero initial velocity. The goal is to keep the poles balanced or prevent it to fall by exerting a force on the cart to make it move. The state of the system on any given point in time is described by:
- The angular position of the poles \theta_{1,2};
- The angular velocity of the poles \dot\theta_{1,2};
- The position of the cart on the track x, which is bounded within [0, X];
- The velocity of the cart \dot x;
- Acting force on the cart F.
These values are known to the system and can be used to determine what force to use next on the cart to keep the poles balanced. The time it is able to, within the bounds of the track, balance the poles is used as a performance measure.
When the NEAT algorithm was developed, it showed that it could solve this problem more effectively and efficiently than that has been done before with other approaches, showing that it had potential for solving more complex problems and was distinct from other already existing approaches.
Algorithm Description
The main idea of the NEAT algorithm is that it combines a genetic evolution strategy with neural networks. Both genetic algorithms and neural networks have been used for solving problems where the behavior of the system investigated is not fully known.
For genetic algorithms, one defines a genome structure, relating input to the solution output in a general way. Then, by means of a performance measure and random influences, successful genomes are combined in new generations to optimize results. There are many variants of genetic algorithms, but all are related in applying evolution theory as studied in the field of biology. Neural networks have a problem solving strategy that is based on ‘training’ the networks, on which we will not elaborate on here.
Both approaches separately have their limitations however. For genetic algorithms, it is often not efficient and without a clear goal on what to optimize as a solution, it cannot perform well. For training neural networks, a topology has to be defined beforehand, which is already a challenging task for complex problems.
With the NEAT algorithm however, the genetic algorithm is not applied to solving the problem directly. It does not evolve a solution of the problem, but rather a solver of the problem. In this case, that is a neural network. The algorithm starts with a minimal neural network possible for this problem. It is minimal in the sense that it only contains nodes for the input and output. Depending on the specific variant of the algorithm used, the initial neural network is fully connected between the input and output or only minimally connected. Then the evolution process starts with generating new neural networks which are then evaluated to determine how the network scores against performance measure. The evolution of networks consists of both topology (adding and removing nodes or connections) and altering connection weights and node biases.
Application to simple problem
To check how this will work on our problem, we applied the NEAT algorithm with a Python implementation to our test model introduced above with three starting nodes and a single goal node. Between these nodes, there are nine roads. For a first implementation, we define our problem with discrete time steps, where we assume a driver completes a trip over a road connection within exactly one time step. We define our Neural Network for this problem with three input nodes, representing the starting distribution of cars in the starting nodes, and 9*T output nodes, where T is the number of time steps we look into the future. These output nodes represent a matrix where for each time step a number determines how many cars we send onto that road. For now, to keep it simple and to enable manual checks, we define the road capacity to be 1 car per time step. This means that the matrix will consist of ones and zeros, indicating for each time step and each road whether the system will send a car on that road or not.
For each generation of networks the algorithm produces, we test its fitness. We do this by evaluating the network a number of times with random starting distributions, and then simulating those starting distributions over time with the output the network provided. The network is considered to be more fit than another when the average time (over all test runs) it took to get the cars to the goal is less than the average time the other network clocked. When a solution failed to send all cars to the goal in T time steps, it is penalized in such a way that its fitness will always be less than a solution that was able to send all the cars to the goal.
When running the algorithm this way, we indeed saw that it learned a strategy and that average (and best) fitness was increasing over the generations.
Further application with traffic simulation
Now that we see we get reasonable results with the simple test model, we turn to more realistic simulations. For this, we want to replace our simple 4-state model with a traffic simulation program, SUMO. SUMO, Simulation of Urban MObility, is a road traffic simulation package. It has a large variety of applications, from simulating new traffic light algorithms to simulating way larger, more global networks. More specifically, with SUMO we can simulate traffic flows and traffic jams to deal with, instead of with restricted discrete distributions of cars.
The model changes a little bit. The Neural Network still has three input and 9*T output nodes and is still evaluated with NEAT. However, the fitness can now be simulated more in a more realistic way using SUMO. It uses the 9*T matrix to know how many cars should be sent in which direction for each time step. Using e.g. the capacity of the roads and possibly arising traffic jams, it knows how long it takes until all cars reach the goal. This can serve as a more realistic fitness which is used to evaluate the neural networks.
Extending the model with more goals
The next step in making the model slightly more realistic, is adding more goal cities. In the current model with four cities and nine roads, only one of the cities served as a goal. It changes the topology of the neural network: it has 4*G - G input nodes (G: amount of goal cities), telling how many cars need to move from one of the four cities to one of the G goals (without cars moving from a goal to the same goal). Furthermore, the amount of roads increases to 12 since people need to move in both directions on all roads now. Lastly, the amount of output nodes increases drastically: it will now have 12*T*G output nodes, telling at each time step T how many cars of the cars to goal G need to go to which road. The rest is still the same: SUMO will make a simulation based on the output nodes of the neural network, which will determine the fitness.
Testing an implementation
Introduction
Testing an implementation of an algorithm is sometimes very hard. It returns a certain solution but how do you know when a certain solution is the best one and what kind of graph do you have to use in your test cases. In this part of the wiki we will explain more about testing our implementation.
Comparing multiple solutions from algorithms
To check if a solution is indeed the optimal, you can compare it with other solutions of the same algorithm or with the solutions of a different algorithms.
How to compare
When comparing solutions of different algorithms and the same algorithm you must be sure that the comparison is valid. A comparison is only valid if they refer to the same situation (thus the same graph, the same amount of drivers and the same destination). If for example you conclude that your algorithm is bad because it returns a different total driving time for France than for Germany, then your conclusion is wrong because indeed the optimal driving time is different for France than for Germany, so it has nothing to do with your algorithm. This doesn’t mean that you cannot use different situation. Of course you can use different situations, however only compare the solutions for France with other solutions for France and only compare solutions for Germany with other solutions for Germany.
Different behavior?!
When comparing different solutions for the same/different algorithms you have to look at the total driving time of the optimal solution. Furthermore for comparing the same/different algorithms you might also take a look at the behavior of a solution, however don’t conclude that one of the solutions is bad because it haves different behavior. Because the total driving time might be the same for solutions with different behavior. To illustrate this we will show a graph of a 3D function:

Suppose our Artificial Intelligent algorithm has to find the solution with the lowest value and suppose it concludes that (0, -5) is the best solution and suppose some other algorithm concludes that the best solution is (0, 5). Is one of these algorithms wrong because the solution of both algorithms is different? Definitely not, they both found the lowest value 0, however the lowest value occur at multiple places. The same holds for our algorithm, there can be multiple solutions for which the result is optimal. In some of our algorithm you can see that a scalar multiplication of the distribution function that the algorithm returns is also a valid solution of the problem, because it has the same total driving time.
Same Algorithm Comparison
This sound strange, but is a very simple test to check if your algorithm is functioning. Most of our algorithms are stochastic and not deterministic so different total driving times might return as value for the same graph as input. This is not a problem if the total driving time doesn’t differ significantly very much (< 1%), however if they differ a lot then either your implementation is wrong or your idea might not work (however there might also be a local minimum, which is not very likely). If your algorithm passes this test, it is an indication that is behaves well. However you cannot directly conclude that your algorithm works.
Different Algorithm Comparison
Also you might test different algorithms, but be definitely sure that you compare same situations. Because a different formula for traffic jams might change the total driving time a lot. For comparing different algorithms the same holds as for comparing the same algorithms. If the total driving time is different it might not be a problem, however the total driving time may not differ significantly very much. If they do then either one of the algorithms is wrong, but they can also be both wrong. If both of your algorithms pass this test, it is a very good indication that both behaves well. Especially when both algorithms differ very much from implementation.
Test Assumptions
To check if a solution is optimal you might make some assumptions about behavior for the optimal solution. If your solution passes these assumptions it indicates that your implementation is good (but you cannot directly conclude These assumptions are:
One direction traffic
Every road consist of a driveway forward and a driveway backward. If drivers are both send on the driveway forward and the driveway backward that need to go to the same goal then something is wrong with your algorithm. You can easily conclude this by saying that either one of the cities is closer to the goal or it is equal, in which case it is never a good idea to go to the city that is further away from the goal.
More roads is better travel time
Using the same graph with more roads won’t increase the sum of the travel times if everyone follow the orders of the navigation system. If the navigation system uses the same distribution over the roads and not sending anyone over the new roads it would have the same sum of the travel times. Hence if the travel time increases then something is wrong.
Shortest Path Without Traffic Jams
Suppose you assume that everyone takes the shortest path and assume that no traffic jams occur (even when a lot of drivers go over the same road) then you get some total driving time A. This total driving time A is always lower than the total driving time B that the artificial intelligent algorithm will find and moreover the total driving time B doesn’t differ very much from the total driving time A. If the new found total driving time B is 20 times larger than total driving time A then something is wrong.
Choosing a graph
Choosing a graph to run your algorithm on is also important for testing your algorithm and can also help to determine the efficiency of your algorithm.
Predetermined Graph
Using an existing simple graph, like Tetraëder or Complex Rectangle:
Advantages are that these graphs are very small and simple to understand and therefore also more easily to see if a solution is indeed the optimal one. Disadvantage are that these graphs are relatively simple compared to real graphs, also creating a predetermined graph that is very large will cost a lot of time for you to create.


Total Random Graph
You will generate an amount of nodes {a1, a2, …, an} and select an amount of vertices {b1, b2, …, bm}. Every vertex vi will be a connection between {ac,ad} and {ad, ac} where c and d are random integers between 1 and n, if this connection has already been made then new c and d will be generated. An example of this is:

Graphs created by this are indeed total random, however most of the time the properties of this graph are not very good. Like depth of the graph and often a graph is not connected, furthermore it is often not realistic because you have crossing vertices without the option to go from one of the vertices to the other. You can make them more realistic by checking each random graph if it is connected and has a certain depth, however this make this method slower and often they won’t be realistic even if you have some requirements.
RR-Grid
RR-Grid stands for random removal grid. A grid graph is very simple and looks like a square (where each vertex stands for two vertices one forward and one backward):

What a RR-grid basically do is remove some vertices. So let’s remove 10 random vertices (from the 40 vertices), then we get:

The advantages of this method are that the generated graphs are random and have nicer properties than total random graphs and the probability that such a graph is not connected is lower than for a total random graph, however you need a lot of nodes to get a high depth.
References
- ↑ https://motherboard.vice.com/en_us/article/new-ai-algorithm-beats-even-the-worlds-worst-traffic
- ↑ https://newrepublic.com/article/117152/how-sunglasses-and-masks-affect-moral-behavior
- ↑ http://www.jstor.org/stable/2937956?seq=1#page_scan_tab_contents
- ↑ https://poseidon01.ssrn.com/delivery.php?ID=277088114073096116071117080070111102029075010065021082108068008081086094118001076093123061037002058104115002091106127124100113047042021051029118117010113017004083073055060031106106069022002121092074068085069008073099015119093003113083027125077101090089&EXT=pdf
- ↑ https://www.youtube.com/watch?v=vBX-KulgJ1o
- ↑ https://www.swov.nl/sites/default/files/publicaties/rapport/d-2010-02.pdf
- ↑ https://www.swov.nl/sites/default/files/publicaties/rapport/d-2010-02.pdf
- ↑ https://www.theguardian.com/world/2014/may/03/everyone-is-under-surveillance-now-says-whistleblower-edward-snowden
- ↑ https://www.cbs.nl/-/media/_pdf/2016/25/tm2016_web.pdf
- ↑ https://www.wegenwiki.nl/Capaciteit/
- ↑ http://www.asimovinstitute.org/neural-network-zoo/
- ↑ http://nn.cs.utexas.edu/downloads/papers/stanley.cec02.pdf