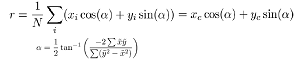Mobile Robot Control 2020 Group 3: Difference between revisions
| Line 277: | Line 277: | ||
==References== | ==References== | ||
(A*) https://github.com/SumiMakito/A-star | |||
(DWA) Fox, D.; Burgard, W.; Thrun, S. (1997). "The dynamic window approach to collision avoidance". IEEE Robotics & Automation Magazine. | (DWA) Fox, D.; Burgard, W.; Thrun, S. (1997). "The dynamic window approach to collision avoidance". IEEE Robotics & Automation Magazine. | ||
Revision as of 09:00, 23 June 2020
Team members:
M.N. de Boer (Martijn)
G.J.L. Creugers (Gijs)
P. Leonavicius (Pijus)
S. Narla (Shashank)
A.L. Nooren (Anna Lisa)
M.K. Salahuddin (Mohamed Kaleemuddin)
Design Document:
Requirements:
The following requirements regarding task performance, safety and software should be satisfied by the simulated PICO robot:
- Task performance
- The robot must be able to recognize target cabinets
- The robot is capable of planning a path and is able to adapt its planned path to unexpected circumstances, for instance a closed door.
- PICO can rotate in place, in order to re-position when in front of a cabinet
- Must be able to announce the completion of the current objective
- The robot should not be inactive for more than 25 seconds.
- The robot has to be able to detect static and dynamic object and present them in the world model.
- Safety
- The robot avoids collisions with static and dynamic obstacles
- PICO must obey the limits on translation and rotation velocity
- PICO should maintain a 5cm Stopping distance from the obstacle.
- Software
- The software is started by a single executable
- The software can be easily updated .
- The User-interaction should be minimal and User-friendly.
Functions:
Input data processing
- Laser range finder interpretation
- Inputs: distance and angle from LaserData Interpreting data generated by the laser range finder, using a 2D SLAM algorithm.
- Odometer interpretation
- Inputs: OdometryData Calculates speed of the mobile robot integrating position values, relays the data to the SLAM algorithm.
- Sensor Fusion
- Combining sensory information from multiple sensors can have uncertainty.This module can help to have reliable information flow to correlate and deconstruct data.
- Vector map data interpretation
- A function used for structuring data obtained from the provided map of the testing area. To be used as
inputs for position estimation and path planning functions.
Mapping world model
- Surroundings detection:
- Comparing the expected surroundings based on the vector map and the output of the LRF interpretation function.
- Obstacle recognition:
- Given the found surroundings, the robot has to decide whether the surrounding are known walls or unknown obstacles as mark them accordingly.
- Position estimation:
- Comparing the expected surroundings using the provided vector map and the outputs of the LRF and odometry interpretation functions.
Control
- Path planning:
- A function based on a Dijkstra’s/ A* / Dynamic programming algorithm. Uses data from the provided vector map and outputs from LRF and odometry interpretation functions. Constantly recalculates the optimal path based on detected obstacles or changes in the environment such as closed doors.
- Movement functions:
- Used for describing routines to be sent as inputs for the base controller of the robot.
- Final re-positioning:
- After the objective position is reached, the rotation of the robot is compared to the required value obtained from the vector map data.
- Signaling function:
- A print output marking the completion of an objective: called once the final state of the path planning algorithm is reached and the correct orientation of the robot is achieved.
- Safety function:
- Constantly running in the background (as a separate process/thread) in order to detect anomalous behavior of the mobile robot and interrupt the operation of the robot if necessary.
Specifications:
- Maintain a distance of 20cm between walls and PICO, stop and reroute if distance is less than 20cm
- Maintain a distance of 80cm from any moving object
- Move at a maximum speed of 0.3m/s while tracking a moving object
- Move forward slightly, if robot has been standing stationary for 30s.
- Maximum speed of 0.5m/s translational, 1.2rad/s rotational
- Position PICO π rad with respect to the cabinet upon arrival
- Visit the cabinets in the required order
Components:
Sensors
- Laser range Finder
- – Provides a set of points in polar coordinates relative to the PICO robot.
- Wheel encoders
- – With this distance translated and rotated can be measured, is however highly sensitive to noise and will require filtering.
Actuators
- Holonomic base wheel
- – It can realise the required degrees of freedom - translation in x and y and rotate about the z - axis without any position level constraints.
Computation unit
- Containing the software module that drives the robot and lets all other components communicate
Interfaces:
Design Document download:
Escaperoom challenge
For the escaperoom challenge a wall-following algorithm has been implemented. This algorithm consists of multiple phases, these phases are visualized in the schematic below.
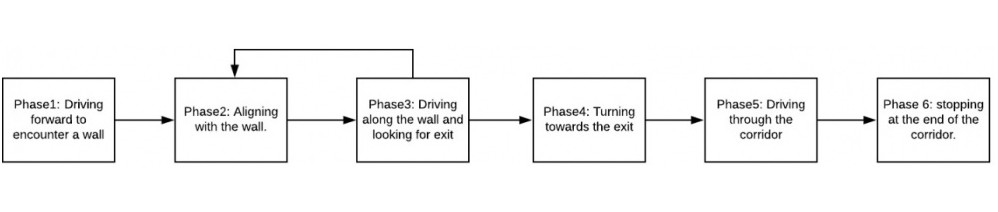
Phase 1:
Since the robot is not aware of its initial position first a wall has to be found before the actual wall following can happen. This is done by driving in a straight line until a wall is detected in a cone of the LRF facing forward. When a wall has been found the software switches to phase 2.
Phase 2:
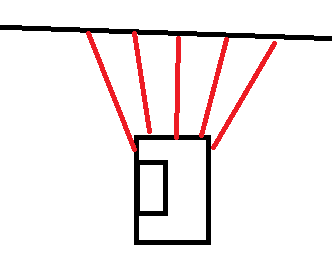
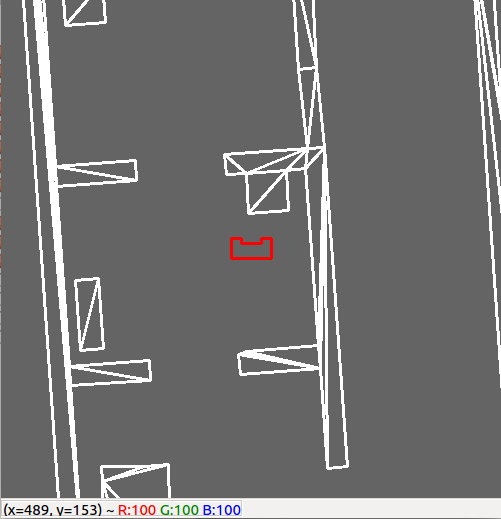
Now that a wall has been localized the next thing is to align the robot parallel to the wall. The estimation of the angular position is done by comparing the values of a number of beams from the laser range finder. In order for the robot to be parallel to the wall, the beam perpendicular to the robot must detect something closer than beams that are ten beams more to the back and to the front. Those beams have to detect some thing closer that beams 10 more beams to the back and front. This condition is illustrated in the picture below. The robot will rotate until this condition is true, then it will move to phase 3.
Phase 3:
In phase 3 the robot will drive along the wall while looking for the exit. In this phase two things can happen. First the robot might sense an obstacle in a cone in front of it and switch back to phase 2. Then it will either align to the current wall if it was driving into it (possibly because of drift) or it will align to the new wall, since a corner has been found. The other option is that a cone to the right of the robot detects no wall meaning that the exit has been found, in that case the robot switches to phase 4.
Phase 4:
Phase 4 takes care of aligning with the exit of the escape room. This is done by rotating the robot until a determined cone of lasers in front of the Pico does not detect a wall anymore. When this is the case it will move to phase 5.
Phase 5:
In this phase the robot will move in a straight line trough the corridor until it reaches the end. It will switch to phase 6 when the outermost laserbeams at either side do not detect any walls anymore.
Phase 6:
When the robot reaches the end of the corridor it switches to phase 6 which will stop the movement to make sure it does not keep going to infinity and beyond.
Video of escape-room simulation:
click here for simulation video where the robot shows it's ability to escape the room.
Result at escape room challenge:
The first gif below is a gif of the actual escape room challenge where the robot failed to exit the escape room. This was due to a minor bug in the software. In self drawn maps, the corridor outwards was not as long as the one from the actual escape room. Therefore the pico did not detect it when it was not close enough to the exit, as the cone would be interrupted by the side of the wall. The roaming nature of the algorithm however made sure it was close enough to the exit. Resulting in this cone being uninterrupted and thus the pico being able to proceed to the next phase. However, in phase 4, the algorithm did also have a too large cone forward where no obstacle should be detected in order to proceed to the next phase, resulting in the Pico perpetually rotating. This cone was changed from 160 to 36 lasers wide. This little fix results in the Pico being able to leave the room. The snippet with the correct code can be found here https://gitlab.tue.nl/MRC2020/group3/snippets/622.
Hospital challenge
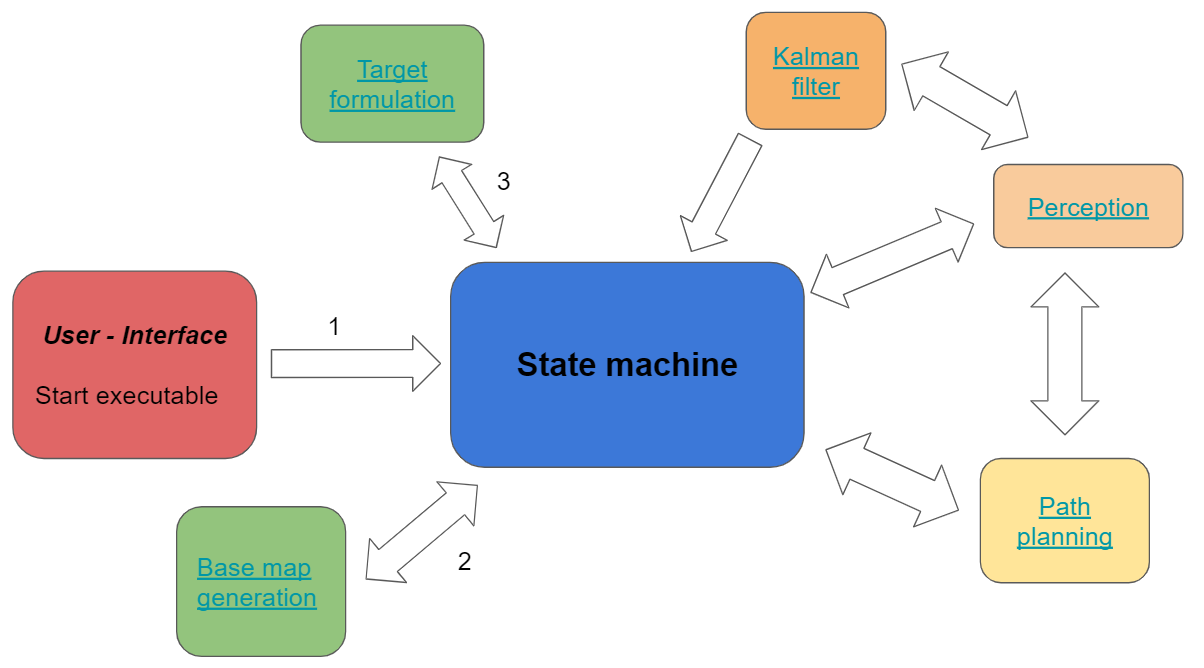
In the escape room challenge the Pico simulation environment has been explored in a relative simple fashion. The hospital challenge is obviously more advanced, but some modules can be adjusted and used again. A schematic visualization of the world model for the hospital challenge is shown below. The separate modules will be elaborated in the next paragraph.
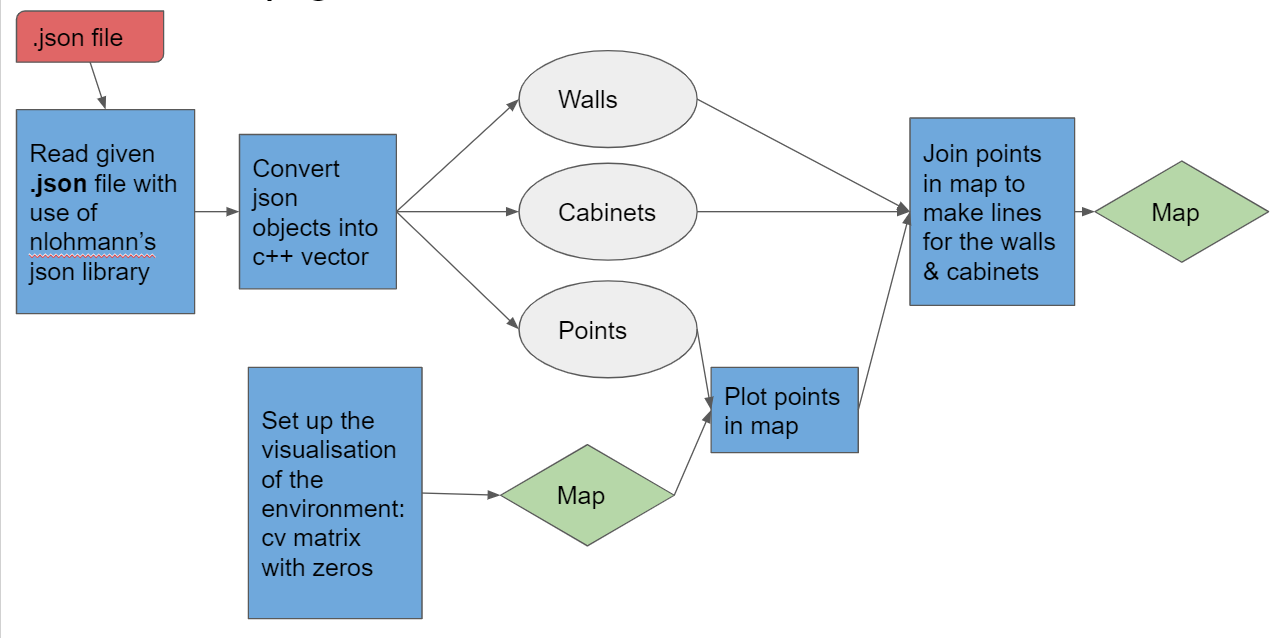
Base map generation
The pre-known layout of the hospital is given to the system in the form of a .json file. From this .json file features like walls, cabinets and points are extracted and converted in a map such that Pico can use this map to navigate and update the map on the go with new data. Below a visualization of the base map generation is shown:
PERCEPTION
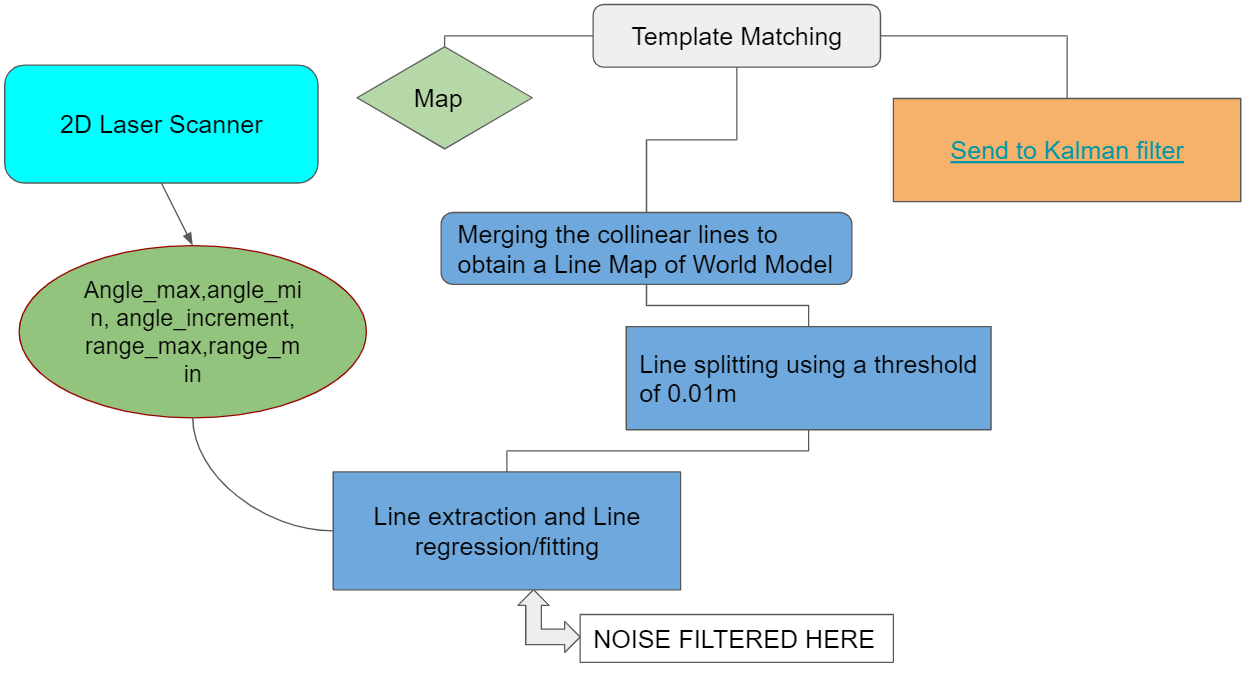
Perception is a process where sensory data is interpreted and used to understand the presented information of the environment. In this case it is used to obtain the specific location in the room from the laser scanner data. The perception process is showed in [figure XX] and contains the implementation of a Split and Merge and Template Matching algorithm. After the Template Matching algorithm, a (x,y, theta) location on the map is send to the Kalman filter to compare the obtained location from the laser scanner data with the location from the odometry data. After this comparison, the output will be a (x,y,theta) location of the robot in the room. In the next sections the to be used Split and Merge and Template Matching algorithm are discussed.
Split and Merge Algorithm
This most important module for the robot is to uniquely identify itself inside the map with a certain position and orientation (x,y,Theta)
1.Dead-reckoning — a method that uses odometry data.
2.landmark positioning — finding the exact position by measuring the distance to obstacles in the environment.
3.sensor-based navigation — utilising a variety of range scanners to build a map of a visible area. Then it is compared with the global map to find the current position.
other methods — GPS or vision systems.
Since we did not have access to the map until a week before and we do not have GPS or vision system, we proposed to use a combination of 1 and 3.
The LRF data is used to extract valuable information such as lines and corners from the LRF data we planned to use Split and Merge algorithm and generate a local map of what the robot perceives. This map will then be compared with the global map using template matching to get an estimate of the robot's position and orientation.
The algorithm that for this was found in the Autonomous Mobile Robots course offered in Eth Zurich here
Firstly the Polar coordinates are converted to cartesian coordinates (x,y) = (r*cosa,r*sina), where r is the range of the product and a is the angle that can be obtained by a = angle_min + (array index)*angle_increment. After converting the individual points to cartesian coordinates,we can now try and represent these points into its line equation: ![]()
We need to find the r and alpha that fits these points into a line. This particular process is called line fitting which is carried out by the fitline() function from the code snippet. This function is trying to reduce the least square error between the individual points (xi,yi) and the line equation that represent the line passing through this point. Which is denoted below:
Hence by taking the gradient of the least square error w.r.t r and alpha, we get the formula for r and alpha that best fits a set of points as given below which is as given below:
This fitline results in many lines that are formed but when there is for example a corner ahead or an intersection then this would lead to multiple lines forming at that place and so in order to split these lines a function called splitlinerecursive() is used to do this operation to distinguish between multiple lines.
After creating multiple lines, the job is not done yet. We need to make sure that there is one unique line representing the points and not a multitude of lines spread across as points. So, we need to merge the collinear neighbours and this is done by the function mergecollinearneighbours().
Finally the function extractlines() is called inside the loop of while(io.ok()) to perform the split and merge algorithm over every sampling time and store it in a matrix and send it to the template matching algorithm to give position estimates of pico.
Template Matching
The template matching algorithm is a wide used computer vision technique to find areas of an image that match to a template image. In the perception process the laser scanner data is processed to an image of the near environment, which is with use of the template matching algorithm matched to the known map of the room. For the implementation of the algorithm the OpenCV library is used, this library contains standard functions to perform the Template Matching method. To execute this method, two functions are of main importance: matchTemplate() and minMaxLoc(). The first function slides the template image over the source image and compares the template against overlapped image regions in the source image. There are six comparison methods defined to choose from, these are futher defined in [source: https://docs.opencv.org/2.4/modules/imgproc/doc/object_detection.html?highlight=matchtemplate#matchtemplate]. After the comparison is done, the best matches can be found as global maxima or minima, depending on the method. To find this specific maximum/minimum value the minMaxLoc() function is used. The function returns the the minimum and maximum element values and their positons. This position can be used as the top-left corner of the rectangle which represents the template image.
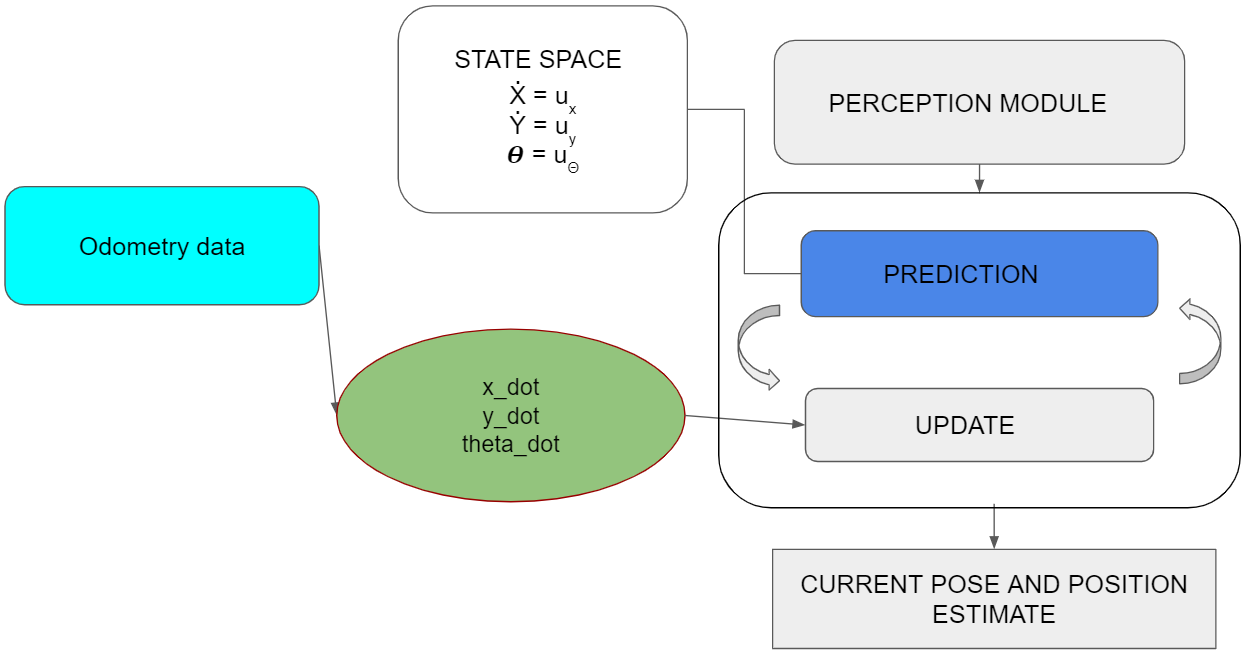
Kalman Filter
To merge the odometry data into position estimation a Kalman filter is implemented. The Kalman filter is a usual choice to filter the noisy signal from the odometry data that takes into account the uncertainty and gives close to accurate state measurements along with future predictions.Another benefit of the Kalman filter is that knowledge of a long state history is not necessary since the filter only relies on the immediate last state and a covariance matrix that defines the probability of the state being correct.
The Kalman filter depends extensively on linear algebra with it's prediction and update equations. C++ does not yet have a standard library to handle matrix operations as efficiently as MATLAB. Hence, to make the implementation easier, Armadillo [1] was used.The library can handle matrix operations through it's in-built classes.
Since PICO robot is a linear system, the state space equations can be predicted easily. The noise covariance matrix and process covariance matrix are diagonal matrices that can be initially set to a predefined value and later converges to the correct value based on the Kalman gains.
Target formulation
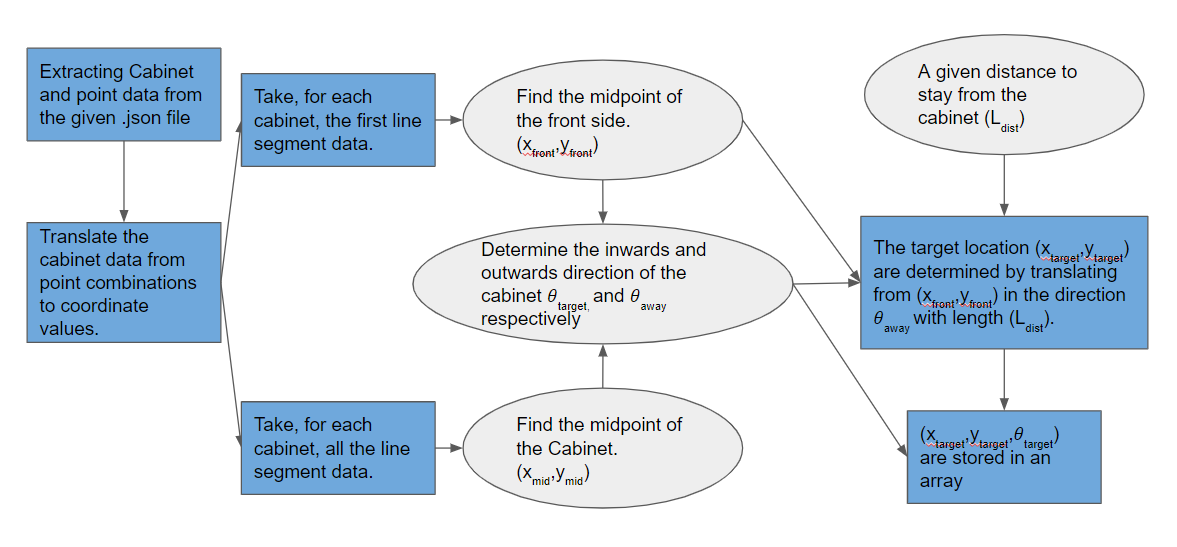
In order to make a good path from the start point to the first cabinet and so on, the pico needs to have a list of target positions it needs to visit. The process of determining this list is discussed in this section. Firstly the point data from the .json file is stored in a 2-by-n array, where n is the amount of points in the .json file. The location in the array notes which point it is. After that the Cabinet data is stored in a three dimensional m-by-4-by-2 array, where m is the amount of cabinets. The first dimension being the cabinet number, the second dimension being the wall number of the respective cabinet and the final dimension being the points of that respective wall. Thus each cabinet is a bundle of 4 combinations of points.
After constructing the cabinet and point arrays, the point values are translated into their global coordinates, creating a m-by-4-by-4 array. Here the third dimension changed from 2 to 4 since each point contains an x and y value.
To determine the midpoint of the whole cabinet, the means are taken from all the x coordinates and y coordinates of the cabinet array respectively.. This then results in a m-by-2 array, containing the x and y coordinates of the cabinet. In order to determine the midpoint of the front of the cabinet, the means of the coordinates are taken from only the first wall of the cabinet, since the first wall is always the front.
To determine the direction outwards of the cabinet, the x and y coordinates of the mid point of the cabinet are subtracted from the coordinates of the midpoint of the front and are then normalized. The inwards direction is simply the inverse of the outwards direction.
The x and y coordinates of each target location is then determined by translating from the front of the cabinet in the outwards direction with a predetermined length. This length is taken to be 0.5 meter, since the pico is about a meter wide and thus it can freely rotate after confirming it has done its objective at the cabinet. The inwards direction is converted to an angle in radians and stored as the third coordinate of the target. Ultimately a m-by-3 array is made containing the x, y and theta coordinates of each of the positions in front of and looking at the cabinet.
When starting the pico an array of cabinet numbers is given. This array is an input of this algorithm. After the final array from the alinea has been made, a new array k-by-3 array (where k is the amount of target cabinets)is generated containing all the position coordinates of the target cabinets in the desired order. This array is then given to the next part of the system. The snippet containing the code is given here https://gitlab.tue.nl/MRC2020/group3/snippets/623.
Path planning
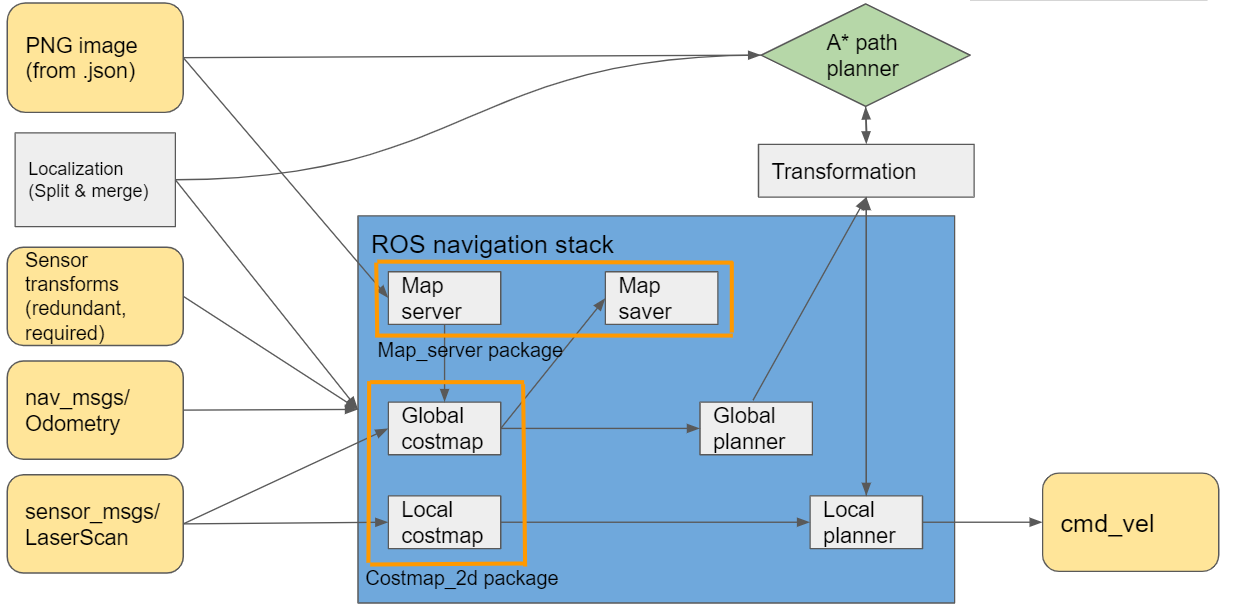
During the course of this project several changes have happened to the way path planning was implemented. Firstly a separate C++ library for an A* algorithm was adapted (_____insert reference (A*) here______), unfortunately implementation issues with C++ and OpenCV (is this correct?) have stopped the group from using this algorithm. The choice was made to completely switch to using the ROS Navigation stack for all path planning purposes. The Navigation stack is an extensive collection of ROS packages meant to fully cover all path planning and obstacle avoidance problems.
The default algorithms for path planning were used: Dynamic Window Approach (DWA) as the local planner and Dijkstra´s algorithm as the global planner. An overview of these algorithms is provided below.
Local planner algorithm
DWA is an algorithm which works in the velocity space, and optimizes for circular paths only (_____insert reference (DWA) here______). The algorithm uses known constraints of velocities and accelerations in order to calculate the appropriate path segment which will result in no collisions before the next recalculation is completed. An advantage of this algorithm is that it results in a slow movement when near obstacles or the final navigation goal, but a disadvantage is that only circular arcs are considered and in some cases this results in movements
Global planner algorithm
Dijkstra´s algorithm is a classical solution and is easy to understand, it computes the shortest path by evaluating and updating costs to each adjacent grid point on the known global cost-map. A graphical representation of the algorithm is presented in (reference gif dijkstra). An important thing to note is that the global planner within the Navigation stack consists of two separate parts: the Dijkstrta´s or A* algorithm, which computes the shortest path and a ¨potential field¨ calculation, which adjusts the path in order to take into account the known obstacles along with the defined inflation radius. There is a reason why Dijkstra´s algorithm is recommended in maps, which are not too large: due to the way Dijkstra´s algorithm works, a much larger potential field is calculated, when compared to A*, which provides more data for gradient descent optimization of the original path, this in turn results in smoother global trajectories.
Ros stuff
One of the main challenges in this project was learning enough about the inner workings of the Robot Operating System in order to successfully implement the Navigation stack.
The original goal was to implement a scan matching algorithm paired with an extended Kalman filter to provide localization for Pico. Unfortunatelly this did not succeed and the choice was made to switch to the Adaptive Monte Carlo Localization package, which is an algorithm based on particle filters.
The starting area was known approximately, thus an initial pose estimate could be provided by choosing center of the start area as the inital coordinates. In order for localization to work suitable covariance values for x, y and theta coordinates (reference insert picture of covariance or something) had to be provided. This allowed Pico to localize pretty quickly and start moving towards the goal. There was only one issue with this approach: if the navigation goal was close to the starting area of Pico (for example cabinet number 0), the robot would get lost, as it believed the goal was already reached before completing the localization.
Recovery behaviors ROS Navigation stack incorporates two recovery behaviors: rotation in place and local cost-map clearing. The initial recovery behavior is to clear the saved global cost-map updates (by default, any obstacle updates further than 3m away are eliminated). Unfortunately this first recovery behavior rarely improves the situation, it would be much more applicable in a real world scenario, where the cost-map gets cluttered with much more data, than in a simulation environment. After clearing the cost-map updates, Pico performs a rotation in place in order to clear out the surrounding space, lastly if this does not succeed, the final behavior is to completely clear the local cost-map and perform another rotation in place, which repopulates the local cost-map and hopefully results in a viable local trajectory being found.
Recovery behaviors are started if one of the following conditions are met: an oscillation is discovered, no global plan is received for a set amount of time or the local planner fails to find a valid velocity command for a set amount of time. In our case, recovery behaviors were started mainly due to the usage of the DWA algorithm for the local planner and sub-optimal settings for the cost map inflation. Pico would attempt to pass too close to the obstacles, which has a chance to result in the DWA algorithm planning a very small trajectory arc, which would be registered as an oscillation. After performing the first rotation in place, an acceptable trajectory was be found, but Pico would again attempt to pass too close to the obstacle thus repeatedly entering the recovery behavior. Unfortunately, during the final Hospital Challenge Pico got stuck in such a loop for more than a minute, thus resulting in a cancellation of the second challenge run. There are two main ways to circumvent this: increasing the inflation radius and adjusting the cost scaling factor parameter, but testing showed that adjustments of the cost scaling factor resulted in very minimal changes in trajectory and at the same time the inflation radius could not be increased, as that resulted in global path planning issues, which are discussed in the following paragraph.
reference: http://www.willowgarage.com/sites/default/files/icra2010_marder-eppstein.pdf
Bugs The inflation radius was set to 0.25 (while the Pico radius along the largest diagonal is equal to 0.224). The difference between the two radii is alarmingly small and as mentioned before it resulted in unwanted errors during navigation. The reason why this setting was used is tied to the navigation goals. The coordinates for target positions in many cases were rather close to the wall and if the target was placed within the inflation radius from a wall or cabinet, Pico would refuse to plot a global path and simply abort the whole navigation procedure. An attempt to remedy this error was made by adjusting the tolerance parameter of the global path planner, which seemed to work, but resulted in Pico plotting a path rather far away from the ideal position (a slightly exaggerated example of this is shown in (figure reference))
Add costmap description, parameters, layer descriptions.
Code snippets
References
(A*) https://github.com/SumiMakito/A-star (DWA) Fox, D.; Burgard, W.; Thrun, S. (1997). "The dynamic window approach to collision avoidance". IEEE Robotics & Automation Magazine.
Hospital Challenge Demo
click here for simulation video where the robot shows it's ability to Navigate the hospital environment.