Embedded Motion Control 2014 Group 11
Go back to the main page.
Group Members
| Name: | Student id: | Email: |
| Groupmembers (email all) | ||
| Martijn Goorden | 0739273 | m.a.goorden@student.tue.nl |
| Tim Hazelaar | 0747409 | t.a.hazelaar@student.tue.nl |
| Stefan Heijmans | 0738205 | s.h.j.heijmans@student.tue.nl |
| Laurens Martens | 0749215 | l.p.martens@student.tue.nl |
| Robin de Rozario | 0746242 | r.d.rozario@student.tue.nl |
| Yuri Steinbuch | 0752627 | y.f.steinbuch@student.tue.nl |
| Tutor | ||
| Ramon Wijnands | n/a | r.w.j.wijnands@tue.nl |
Time survey
The time survey of this group will be hosted on a Google drive. Therefore, all group members can easily add information and anyone can see the up-to-date information. The document can be accesed by clicking this link: time survey group 11
Planning
Week 1 (28/4 - 4/5)
Finish the tutorials, including
- installing Ubuntu,
- installing ROS
- installing SVN
- get known with C++
- get known with ROS
Week 2 (5/5 - 11/5)
Finish the tutorials (before 8/5)
- Setting up an IDE
- Setting up the PICO simulator
Work out subproblems for the corridor competition (before 12/5)
Comment on Gazebo Tutorial
When initializing Gazebo, one should run the gzserver comment, however, this can result in a malfunctioning program, i.e. you will get the following message: Segmentation fault (core dumped). The solution for this is to run Gazebo in debugging mode (gdb):
- Open a terminal (ctrl-alt-t)
- Run:
gdb /usr/bin/gzserver
when (gbd) is shown, type run and <enter> - Open another terminal (ctrl-alt-t)
- Run:
gdb /usr/bin/gzclient
when (gbd) is shown, type run and <enter>
Comment on running Rviz
Simular to the Gazebo tutorial, the command rosrun pico_visualization rviz can also result in an error: Segmentation fault (core dumped). Hereto, the solution is to run Rviz in debugging mode:
- Open a terminal (ctrl-alt-t)
- Run:
gdb /opt/ros/groovy/lib/rviz/rviz
when (gbd) is shown, type run and <enter>
Moreover, in order for the camera to work properly, in the Displays view on the left change the Fixed Frame.
Week 3 (12/5 - 18/5)
Finish the corridor competition program.
Week 4 (19/5 - 25/5)
Update the wiki page with current software design. Optimize current software nodes. Determine workload for implementing SLAM and a global controller.
Week 5 (26/5 - 1/6)
A launch file is created to run the multiple nodes at once. Currently, it runs the following nodes:
- Target
- Path_planning
- Drive
To apply the launch file, execute the following steps
- Start the simulation up to and including
roslaunch pico_gazebo pico.launch
- Open a new terminal (ctrl-alt-t)
- Run:
roslaunch Maze_competition pico_maze.launch
Maze competition
The goal of this course is to implement a software system such that the provide robot, called PICO, is able to exit a maze autonomously. Embedded software techniques provided in the lectures and literature need to be implemented in C++. The ROS concept is used as a software architectural backbone.
The PICO robot has three sources of sensor information available to percieve the environment. First a laser provides data about relative distances to nearby objects (with a maximum distance of 30 meter). Secondly, images can be used to search for visual clues. Finally, odometry data is available to determine the absolute position of the PICO.
PICO can be actuated by sending velocity commands to the base controller. The PICO is equipped with a holonomic base (omni-wheels), which provides the freedom to move in every desired direction at any moment in time.
The assignment is successfully accomplished if the PICO exits the maze without colliding with the walls of the maze.
Software design
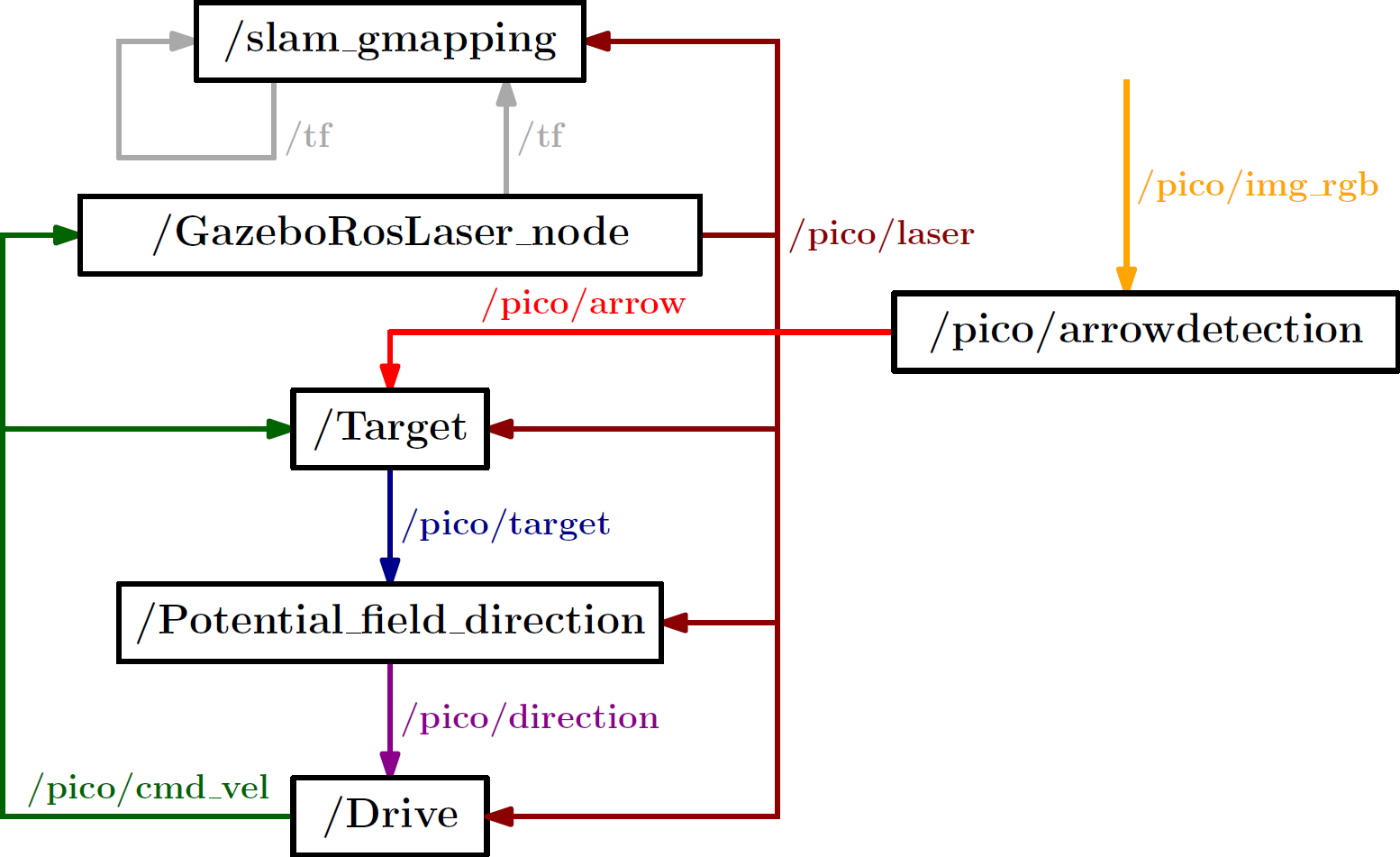
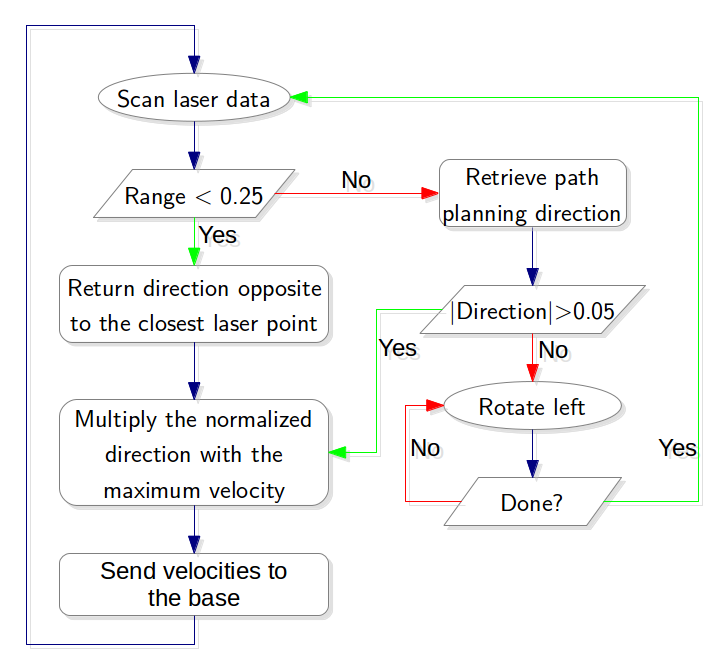
The current ROS node structure is shown in the figure below.
The nodes /GazeboRosLaser_node and /pico/pico_state_publisher are predefined ROS nodes. Currently, four extra ROS nodes are added:
- /Target: This node determines the target where the PICO has to drive to. The node has as input the laser data and velocity commands, and produces a point expressed in relative coordinates. If multiple interesting targets are found, it returns the most left or most right target (which can be chosen before starting this node).
- /Potential_field_direction: From a given target, it produces a path to that target. It generates this path by using potential fields, where walls have high potentials and the target a low potential. It returns a direction where the PICO has to go at that moment in time.
- /Drive: It translates the received direction into a translation and rotation speed. This node is able to change the direction if it notice that the PICO is to close to a wall.
- /slam_gmapping: This node produces from the laser and odometry data a map of the maze. This allows to know the absolute position of the PICO in the maze. Therefore, targets can be memorized to, for example, prevent looping in the maze.
The next table summarize the message types for each used topic.
| Topic name: | Message type: |
| /pico/laser | LaserScan |
| /pico/target | Point |
| /pico/direction | Point |
| /pico/cmd_vel | Twist |
| /tf | tfMessage |
| /map_metadata | MapMetaData |
| /map | OccupancyGrid |
In the following sections, the algorithm used in these nodes will be explained in more detail.
Target: Where should Pico drive to?
The first step in successfully exiting a maze is to be able to detect the surroundings, and identifying where Pico should drive to. This is done in the 'Target' node. This node identifies corridors, junctions and other features of the maze. Next, it determines a target, i.e. the point Pico should drive to, on the basis of these identified features. A first step is thus to identify the various features of the maze.
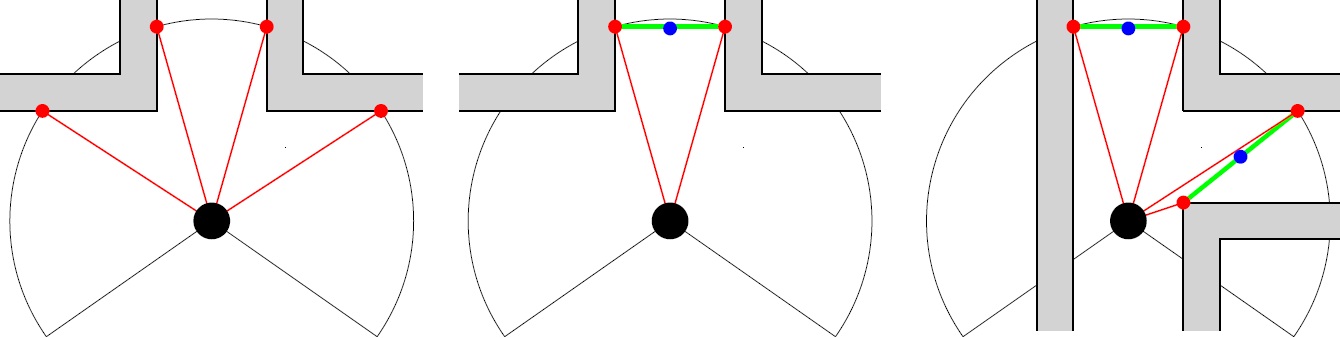
A method is used here based on the distance of Pico to the maze. By drawing a circle with radius R around Pico, and determining those points at which the maze intersects this circle. This process is described below.
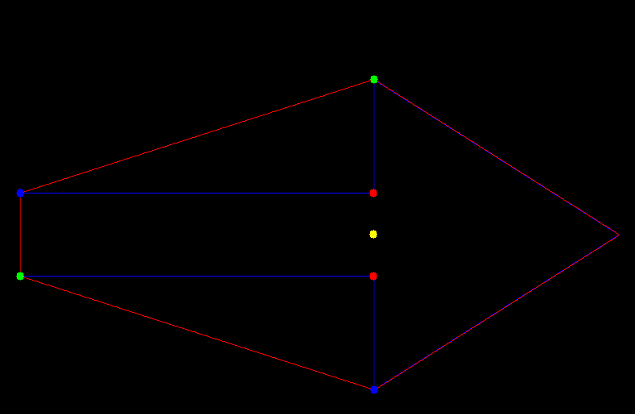
As shown in the left figure below, PICO is positioned in front of the maze. Using a certain algorithm, useless red dots are removed and pairs that represent a hallway are saved. If we take the average of the each pair, we would have exactly found the middle of each hallway we want to drive to. However, there are two more points identified as well, which give us no information about possible hallways.
In the figure below to the right, it can also be seen that hallways to the left or right can also be identified, and in this way, junctions, hallways and dead ends can be identified. The latter one can be identified by the lack of remaining points.
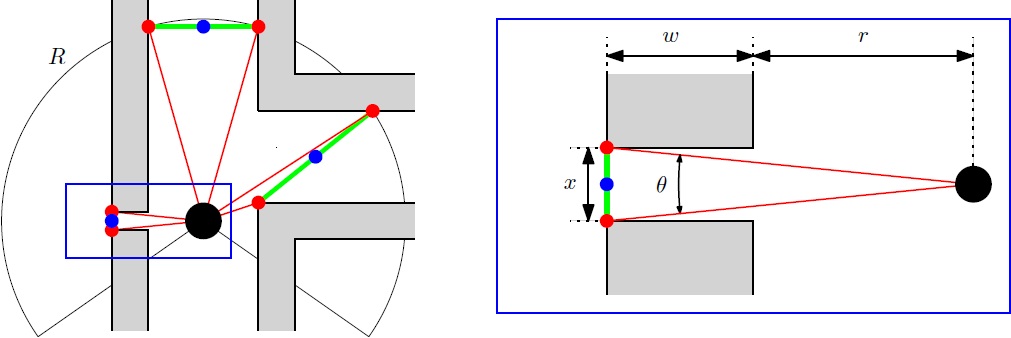
However, a small gap can also be detected and considered to be a hallway, as shown in the figure below. In order to ignore such a gap, the angle difference of the points of a pair are compared with a threshold value. This threshold value is calculated for the worst case scenario: [math]\displaystyle{ \theta=0.1 }[/math] rad under assumption that the Pico is closest to the wall (a distance of [math]\displaystyle{ r=0.25 }[/math] m from the wall), a gap of [math]\displaystyle{ x=4.5 }[/math] cm and a wall thickness of [math]\displaystyle{ w=0.2 }[/math] m (see figure below right). Additionally, by demanding that the distance between the two points of a hallway is large enough (> 0.5 m), the identified hallway will be large enough for Pico to drive through. Note that only the distance criterion is not strong enough, since Pico might look through the gap to outside the maze, which means that the distance between two points can be large, even if the gap itself is only small.
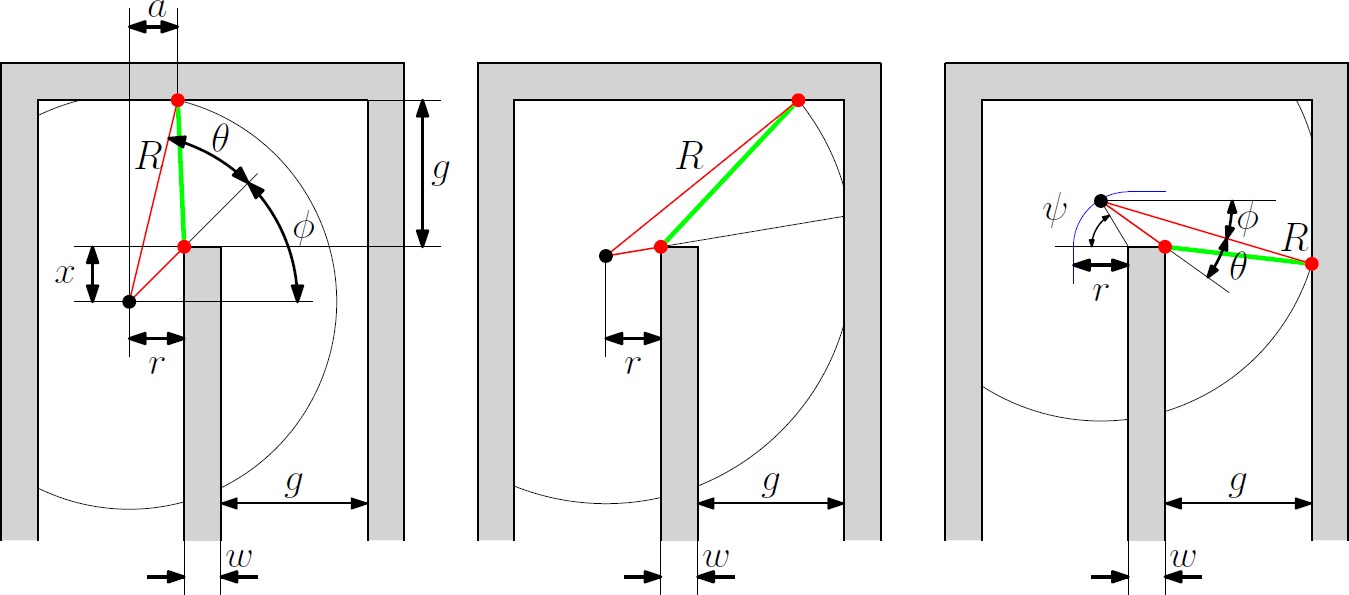
The worst kind of hallway for this detection method is shown in the figure below: a U-turn. From the figure below, it can be seen that the radius R should not be too large; If it is too large, the U-turn cannot be detected and Pico will think that it has hit a dead-end. The left figure shows the radius R and several measures as Pico approaches the U-turn. During this phase, the minimal distance of Pico to the backwall can be calculated using the geometry and the angles [math]\displaystyle{ \theta }[/math] and [math]\displaystyle{ \phi }[/math]. As such, the radius should be smaller than this value, meaning that the maximum of the radius is [math]\displaystyle{ R=1.148 }[/math] m. It is also important that the angle is always larger than the derived [math]\displaystyle{ \theta = 0.1 }[/math] rad. The center figure shows that [math]\displaystyle{ R_{max} \lt r+w+g = 1.05 }[/math] m in order to maintain the red dot at the center wall up to [math]\displaystyle{ x=0 }[/math] m. The right figure shows what happens beyond the point [math]\displaystyle{ x=0 }[/math] m. Again, we can calculate the minimal distance of Pico to the red dot using geometry, keeping in mind the minimum angle of [math]\displaystyle{ \theta = 0.1 }[/math] rad. In this situation the maximum value for the radius is then the smallest one of the three: [math]\displaystyle{ R \lt 1.034 }[/math] m. All the values are calculated with [math]\displaystyle{ r=0.25 }[/math] m, [math]\displaystyle{ w=0.2 }[/math] m, [math]\displaystyle{ g=0.6 }[/math] m.
Thus, the radius for this method should be [math]\displaystyle{ R = 1 }[/math] m in order to be able to detect U-turns as well. This causes a problem when entering a junction with a hallway width of [math]\displaystyle{ g \gt 1.5 }[/math] m, since Pico will not be able to detect the other side using this radius, and thus won't detect any corridor to the left or right. In order to always see the wall in a crossing with hallways of 1.5 m, the maximum distance of Pico to the nearest wall is ([math]\displaystyle{ \sqrt{0.75^2+1.5^2} = }[/math])1.67 m. Therefore a second radius is added of [math]\displaystyle{ R_o=1.7 }[/math] m, such that even on such crossings, a wall will always be detected.
Using these two radii, all hallways are detected and several hallways are detected in twofold (with both the large and the small radius). Now the last step is to select the hallway that Pico should drive to, the target. There are several properties the hallway should satisfy in order to be a potential target:
- the center of the hallway detected by Pico is inside its 180 degrees vision ([math]\displaystyle{ +- 90 }[/math] degrees),
- the corridor pair does not represent a dead end.[math]\displaystyle{ {}^* }[/math],
- the angle of the pair is larger than [math]\displaystyle{ \theta = 0.1 }[/math] rad (as said before),
- the gap is large enough for pico to drive through ([math]\displaystyle{ \gt 50 }[/math] cm).
When there is no point detected, pico will stay at its current position and turn (anti-)clockwise, depending on its favoured direction. When there are more potential targets detected, Pico will follow the one with the largest or smallest angle (depending on its favoured direction). In this way, the target is selected and is send to the path planning node.
[math]\displaystyle{ {}^* }[/math] A corridor pair represents a dead end if no two consecutive points show a step of at least [math]\displaystyle{ 40 }[/math] cm difference in position. This means, if all points are within [math]\displaystyle{ 40 }[/math] cm of their neighbours, there can be no hallway and thus, the corridor is a dead end.
Path Planning Pico: Potential Field Approach
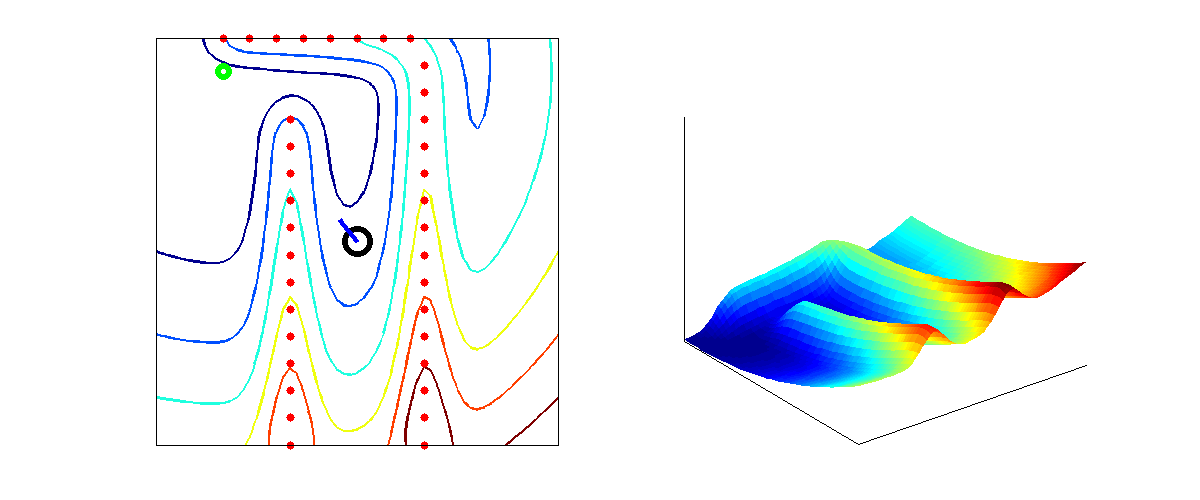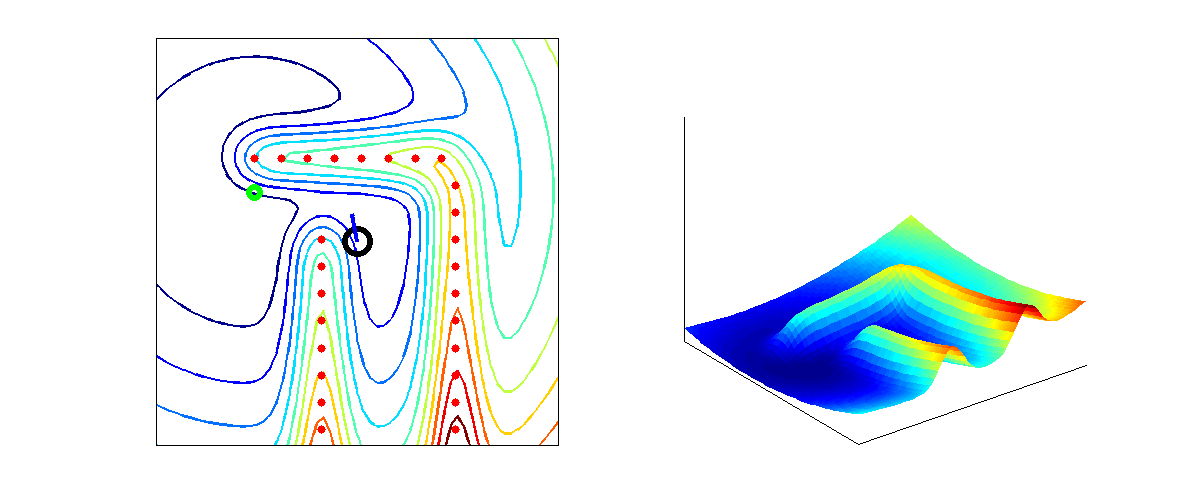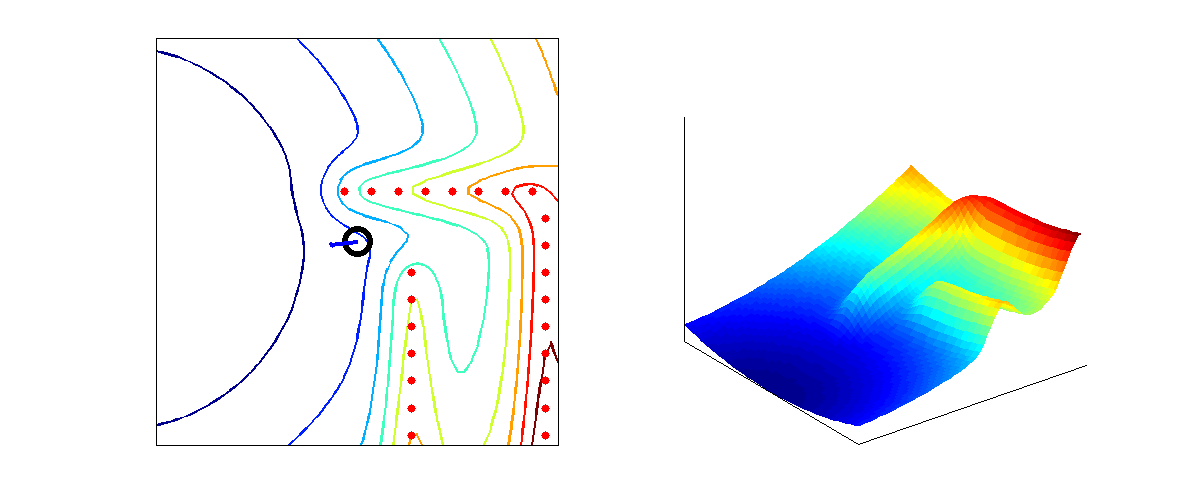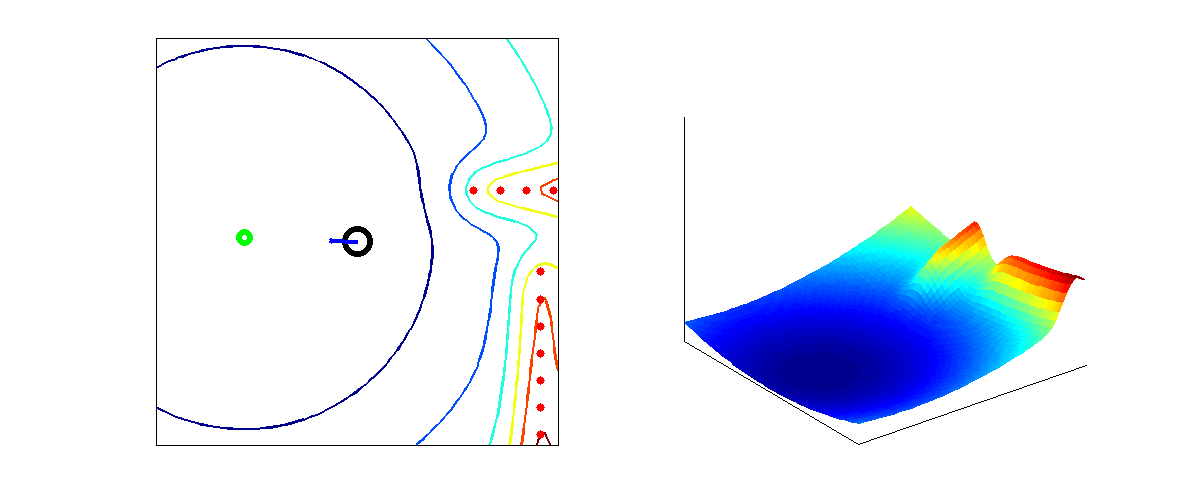
From the higher level control node "Target", Pico will receive a desired local destination. In order to reach this destination in a smooth fashion, a particular path planning method will be employed. This method is based on artificial potential fields. The key idea is that the local target (destination point in 2D space) will be the point with the lowest potential. Everywhere around this target, the potential will be strictly increasing, such that the target is the global unique minimum. Any objects as detected by Pico will result in a locally large potential. The path planning can now be based on any gradient descent algorithm as are often used in optimization problems. Because of the ease of implementation, the first order "steepest descend" method will be used. This is equivalent with computing the resulting conservative force as induced by the potential field (think of electrostatics). In the gif below, the main concept is illustrated.
Here, Pico is the represented by the black circle and the smaller blue circle is the target. The potential field generated by the target is simply the euclidean distance squared, i.e,
[math]\displaystyle{ P_{target} = (x_{target} - x_{pico})^2 + (y_{target} - y_{pico})^2 }[/math].
The red spots represent the laser measurement data (in reality, the measurements are not so nicely equally spaced). Each measurement point contributes to the potential field. Because the objects should repulse Pico, each point will be presented some sort of a peak. We considered two different possibilities. The first one is based on a 2D gaussian distribution,
[math]\displaystyle{ r_{object,i} = \sqrt{ (x_{object_i}-x_{pico})^2+(y_{object_i}-y_{pico})^2} }[/math],
[math]\displaystyle{ P_{objects} = \sum_{i = 1}^{1081} exp\left( \frac{ -r_{object,i}^2}{\sigma^2} \right) }[/math],
where [math]\displaystyle{ \sigma }[/math] is a skewness parameter which can be tuned to obtained the desired behavior. Since this can be a bit to restrictive in some cases, a second option is considered, which is based on the response of a RLC circuit.
[math]\displaystyle{ P_{objects} = \sum_{i = 1}^{1081} (A + B r_{object,i}^2)exp\left( -\lambda r_{object,i}^2 \right) }[/math],
where [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math] and [math]\displaystyle{ \lambda }[/math] can now all be tuned to create best behavior of Pico (The gif is based on the latter potential field).
The total potential field now becomes,
[math]\displaystyle{ P_{total} = \alpha_1 P_{target} + \alpha_2 P_{objects} }[/math],
where [math]\displaystyle{ \alpha_1 }[/math] and [math]\displaystyle{ \alpha_1 }[/math] are additional tuning parameters. The steepest descent direction is numerically approximated (this could also be done analytically) by constructing a local grid around Pico and computing the central first order difference in both the x- and y-directions,
[math]\displaystyle{ \vec{\nabla} P_{total} \approx \frac{P(\Delta x, 0) - P(-\Delta x, 0)}{2 \Delta x} \vec{e}_x + \frac{P(0, \Delta y) - P(0, -\Delta y)}{2 \Delta y} \vec{e}_y }[/math].
The direction in which Pico should move is now given by,
[math]\displaystyle{ \vec{D} = -\frac{\vec{\nabla} P_{total}}{\|\vec{\nabla} P_{total}\|} }[/math].
This direction will be send to the "Drive" node which computes the appropriate velocities based on this direction. An attempt was made in include local curvature information of the potential field by approximating the Hessian matrix locally. This so called Newton method may result in faster convergence and hence a shorter path. However, it is well known that this method can be unstable and may for example converge to local maxima or saddle points. Indeed, implementation of the method showed that convergence could not be guaranteed within a desirable time and hence the method is not pursued any further.
Drive: How to move in the given direction
The direction from the "Path Planning" node is send to the "Drive" node. Here, it is determined in what way the Pico will drive, and the resulting velocities are send back to the system. First, there are several boundary conditions for driving Pico:
- Its forward velocity cannot exceed [math]\displaystyle{ |v|_{max} = 0.2 }[/math] m/s,
- Its angular velocity cannot exceed [math]\displaystyle{ |\omega|_{max} = 1 }[/math] rad/s,
- Pico must not touch the walls.
This last condition is most important: if Pico hits the walls, the challenge is over. Thus, the "Drive" node starts with a safety mechanism. At every timestep, Pico scans the distance to its surroundings. If any point is closer than 25 cm, Pico moves directly away from that point, overruling any direction given by the "Path Planning" node. If multiple points are within 25 cm, Pico moves away from the average of the points, making the distance to all points bigger. As said, this part overrules any other direction since it is of utmost importance.
If not point is within 25 cm, however, Pico moves in the direction send by "Path Planning" with maximum velocity (0.2 m/s). Also, if the direction has a y-component, Pico automatically turns toward the direction it is driving. However, it does not turn at full velocity. Rather, it turns at a speed which has a linear relation to the angle of the direction with Pico's current position. In other words, we have that [math]\displaystyle{ \omega = atan(v_y/v_x)/(0.5 \pi)*1 }[/math], with [math]\displaystyle{ v_y, v_x }[/math] the y- and x-component of the direction. The angular velocity is normalized such that Pico turns at full speed ([math]\displaystyle{ |\omega|_{max} = 1 }[/math] rad/s) when the direction is perpendicular to Pico's current orientation.
In this way, Pico always moves at maximum velocity whilst turning when needed. Furthermore, before any velocity is send to base, both the forward and angular velocities are normalized, ensuring once again that the send velocity does not exceed the given maximum velocities. By using this algorithm, it is ensured that Pico does not hit the walls, and uses the given equipment to its full potential.
Alternative approach: driving the Pico without omniwheels
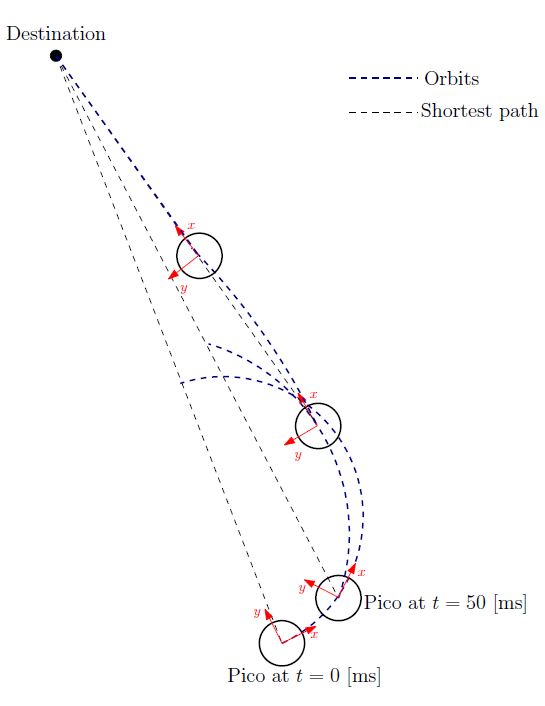
In some simulations, Pico might not have omniwheels available. This means that Pico cannot drive directly in the direction given, since the direction (in general) also has a y-component. There are various ways to let Pico drive from one point to the other without omniwheels, using its two independ velocity componements, namely the translational speed [math]\displaystyle{ \dot{x} }[/math] and its rotational speed [math]\displaystyle{ \dot{\theta} }[/math]. One could for instance first rotate the Pico in the right direction, to subsequently just drive forwards until the destination is reached. However, this can be a time consuming task as the Pico has to stop each time a correction on the direction has to be made. Moreover, when a corner needs to be taken, mutlitple waypoints are necessary to guid the Pico. Therefore, an alternative algorithm is developed, which can react more quickly on directional changes and steers the Pico as fast as possible towards its destination. The concept of this algorithm is shown in the figure to the left.
Here an extreem situation is sketched, to fully illustrated the functioning of the method. In the figure, the pico is shown at various moments in time, where the driving direction (or facing direction of the Pico) is the relative x-direction. Moreover, a destination point is shown in absolute coordinates, however, one must keep in mind that the information fed to the algorithm is the relative destination with respect to the Pico and all calculations are performed on this relative coordinate set.
The general idea of the algorithm is as follow: The shortest distance from the Pico to its destination would simply be a linear path. However, as the pico often does not face that direction, it is not possible to drive with the given velocity componements along this linear path. On the contrary it is possible to descirbe spiral orbit paths which get the Pico as fast as possible on that linear path (see the figure on the left). These orbits are described by:
One can do so by demanding that after a certain time [math]\displaystyle{ T }[/math], which is a function of the sampling time [math]\displaystyle{ T_{sample} }[/math] and the distance to the destination [math]\displaystyle{ L_{d} }[/math], i.e. [math]\displaystyle{ T = f( T_{sample}, L_{d} ) }[/math], the Pico has reached this linear shortest path. In addition, it is demanded that in that time the Pico has traveled to the same point as it would have when it could drive along the linear path with its maximal translational velocity. However, as the Pico moves, the shortest path to the destination changes. As a result, after each [math]\displaystyle{ T_{sample} }[/math] seconds, the orbits are recalculated as shown in the figure to the left, resulting in a smooth path towards the destination.
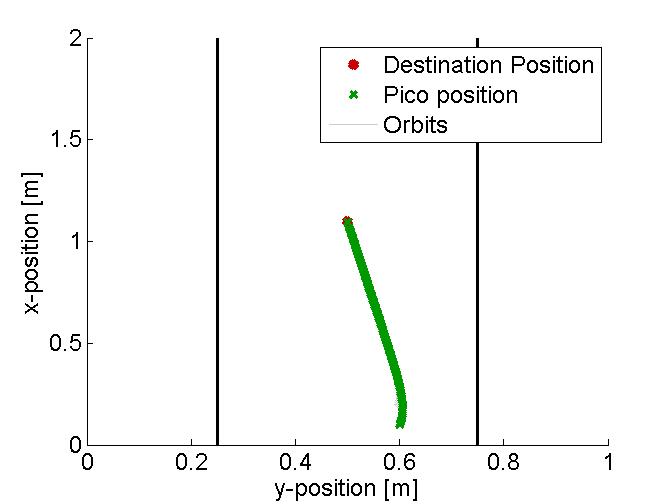
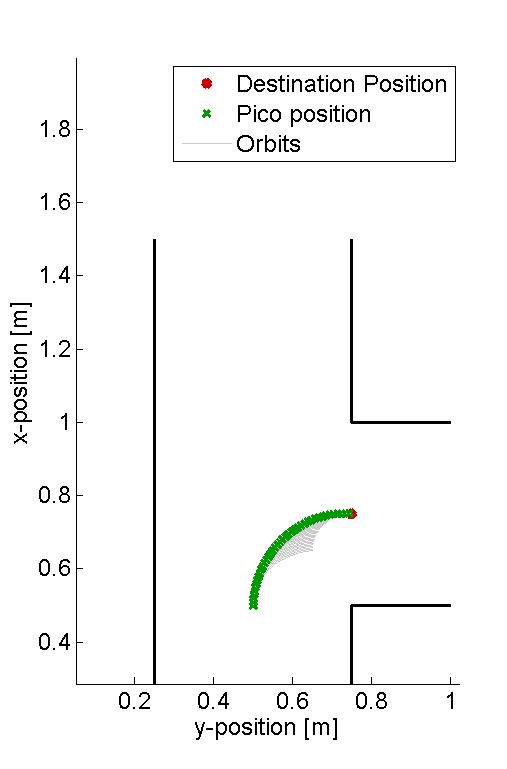
In the figure below, several examples of the working principle of the driving algorithm are shown. In the left figure, an extreem situation is sketched, such that one can clearly see the calculated orbits and the driving path. Such a situation is not likely to happen in the context of this project. The middle figure shows how the driving algorithm can be used to reallign the Pico when it is of center, and the right figure shows how corners can be taken by the Pico. In this latter situation, no intermediate destination points are needed, but are still an option.
Arrow Detection
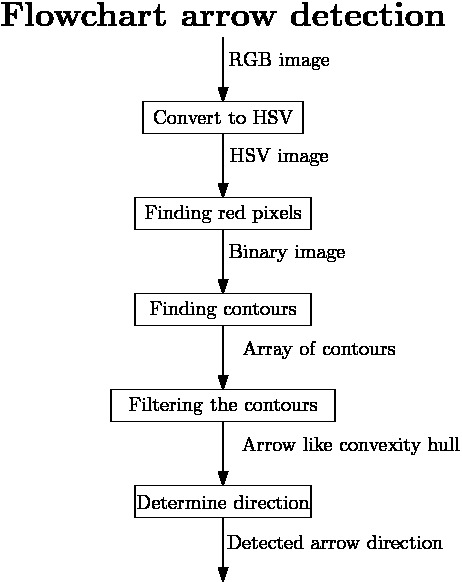
In order to solve the maze faster, it is useful to detect the various arrows in the corridors, guiding the pico towards the exit. Hereto, a separate node has been developed, which can work parallel to all the other nodes, to detect and interpret these arrows. In the figure below to the left, one can see a flowchart of the algorithm used for detecting the arrows. The various aspects for this detection are here below more elaborated.
Detecting the red objects
As it is given that the arrows to be detected are red, a first and obvious step is to detect the red objects in the image. From the pico camera one receives a color image in the RGB format, see for example the left figure below. However, it is easier to filter the image by a certain color when the image is in HSV format. The reason for this is that then the OpenCV function inRange can be used. As a result, the RGB image from the pico is first converted to this HSV format using the OpenCV function cvtColor, see the middle figure below for the result.
Subsequently, the HSV image is used to extract only the red objects in the image. In the HSV color spectrum handled by OpenCV, red is the color with the hue value equal to 0 or 180. Hence, slightly darker red lays in the range H = 170-180, while a lighter red color has an hue value H = 0-10. As a result, using only one threshold value to filter the image may result in missing red objects. Therefore, to ensure all the red arrows are seen, the HSV image is filtered twice with the inRange function, and the results of both filters are added up. The resulting image is a socalled binary image, which only exists of white and black pixels, where the white pixels represent the red detected objects, see the most right figure below.
Finding the arrow
Since multiple red objects could exist in the original RGB image, only filtering on the red color is not enough to detect the desired arrow. Therefore, the resulting binary image is filtered, to get rid of the unwanted red objects. Hereto, contours are used to determine the shape of the various detected red objects. In the binary image, contours are calculated around each object, which essentially matches the outer edge of the object. Now a first filter step can be applied, as the area of the contours can be calculated using the function contourArea. By demanding that the area must be larger than a certain threshold value, smaller detected objects can be eliminated from the binary image. However, choosing this area value too large will result in a late or even no detection of the arrow. As a result, only using the area filter will not be enough to eliminated all the unwanted red objects.
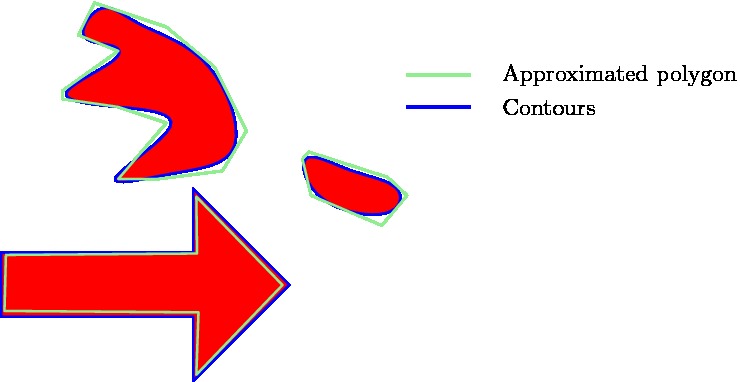
Therefore, all the found contours are approximated by a polygon using the approxPolyDP function in OpenCV. As the arrow has a standard shape, one knows that the approximated polygon will contain 7 vertices (or close to that number), while random red objects will have many more or less. This is illustrated in the figure to the right, where one can see a good approximated arrow, a contour which needs a high degree polygon for the approximation and a contour which only needs a low degree polygon for the approximation. By using this polygon approximation, one can actually get rid of must of the unwanted red objects, however, this filtering method is not waterproof, and hence more filtering steps are needed.
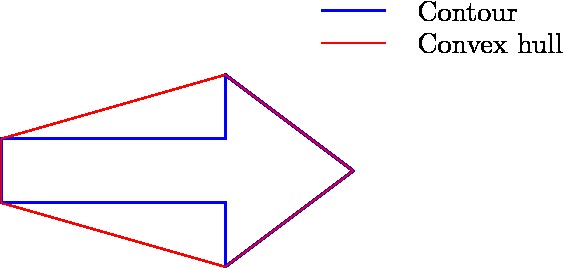
As a result, the principle of convex hulls is used as a next step to filter the binary image. For each of the remaining contours, a convex hull is calculated, which is the smallest convex set containing all the points of the detected object. In the figure below, the convex hull for the arrow is shown. As it can be seen, the contour and the convex hull have many similarities, however they differ in an essential point, the area they span. More precisely, when determining the ratio between the area of the contour and the area of the convex hull, for the arrows to detect it holds that [math]\displaystyle{ \frac{\text{area contour}}{\text{area convex hull}} \approx 0.6 }[/math], which is quite a specific number for the arrow. Therefore, as a final filtering step, this ratio is used to eliminate the final unwanted red objects. By combining the three main filtering steps, one can ensure that the only remaining contour in the binary image is the contour belonging to the arrow to be detected.
Determine the direction
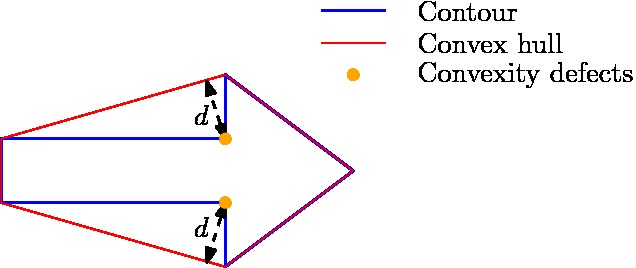
As the binary image has now be filtered such that only the contour of the arrow is remaining, one can start focusing on determining the direction the arrow is pointing. Hereto, again the principle of the convex hull is used, or more precisely, the principle of convexity defects. Convexity defects are in principle the points which have the largest deviations from the hull with respect to the contour. In the figure below on the left, one can see what the convexity defects are for the arrow, if the search depth [math]\displaystyle{ d }[/math] is choosing high enough. These convexity defects can then be used determine the midpoint of the arrow. The direction in which the arrow is pointing subsequently determined by measuring the amount of contour points to the left and right of this midpoint. As the arrow pointing part will contain many more points then the rectangular part of the arrow, the direction can thus be easily qualified. An overview of the contour, the convex hull, the convexity defects, and the midpoint as calculated by the algorithm can be seen in the figure below to the right.
Results
Below one can find several Youtube videos which demonstrate the working principle of the arrow detection algorithm.
SLAM
To be able to tackle any maze the use of Simultaneous Localization And Mapping (SLAM) is considered. When, for example, an arrow is detected and followed, it is possible to get stuck in a loop in the maze. Slam is a technique that makes it possible to make an accurate estimate of the position of the robot relative to a certain point. This makes it also possible to make a map of the environment because all detected objects can be stored relatively to a certain point.
How slam works
For slam to work properly two sensors are used. First the odometry sensor, which estimates the position and orientation over time, relative to the starting location. This sensor however is sensitive to errors due to the integration of the data over time, this will therefore not be accurately enough to determine the position of the robot. So a second sensor, the laser-scanner, is used to help to improve this estimation. Slam works in different steps visualized in the figure below. The triangle represents the robot an the circles represent the landmarks.
1. First the landmarks are detected using the laser-scanner. The landmarks could in this case be the walls and/or corners of the maze. The position of these landmarks are then stored relative to the position of the robot.
2. When the robot now moves, the position and orientation is estimated by the odometry sensor, so the robot now 'thinks' that it is here.
3. The new locations of the landmarks relative to the robot are determined, but it finds them at a different location then where they should be, given the robots location.
4. The robot trusts its laser-scanner more then it trust its odometry, so now the information of the landmark position is used to determine where the robot actually is. Eventually also this new position is not the exact position of the robot because also the laser-scanner is not perfect, but the estimation is much better than relying on the odometry alone.
Gmapping
In ros there already is a package, called Gmapping, available which builds a map using SLAM. So this will be used to obtain the position of pico. Because a map is also provided, it might also be possible to use this map for finding walls and corners, and therefor detect the junctions. When using gmapping on pico the most important part is to determine the right parameters to get the most accurate results.
Algorithm
The advantage of SLAM is now that it is possible the store the position of objects relative to a certain point. This will be used to store the position of every junction that is encountered. Secondly for each junction every corridor is marked as: entered, open or dead-end. When then a junction is crossed again, this information is used to determine which exit will be taken and the information can then be updated. Below an algorithm, that can be used, is visualized. This algorithm starts with finding a junction. When it finds one the robot will start to drive to that junction. Then it will choose one of the open corridors, based on an algorithm such as always the most left corridor, or the information delivered by an arrow can be used. When the robot drives into a corridor it will now not only start to detect a junction, but also a dead-end and a finish. When the finish is found the robot can drive out of the maze. When a dead-end is detected the robot will return to the previous junction and mark the corridor as a dead-end. And when a junction is found the robot will drive to that junction and the algorithm starts again, unless the found junction is already encountered, which will then be treated as a dead-end. This algorithm should be able to find the exit without getting stuck in a loop.
Implementation of gmapping
In the video below (click on the picture to be redirected to YouTube), a succesful implementation of gmapping is shown. The gemapping node is launched with the following parameters:
rosrun gmapping slam_gmapping scan:=/pico/laser _odom_frame:=/pico/odom _base_frame:=/pico/base_link _maxUrange:=2.0 _map_update_interval:=2.0
First, the default frames of scan, odom_frame and base_frame need to be changed with the correct pico frames. Next, the maximum used range is set to 2.0 m. Finally, the update interval of the map is set to 2.0 s. A lower update interval requires more computation power. The video shows also that the generated map may contain errors. When, for example, the omniwheels slip, the odometry data is not perfect accurate any more. This results in a map with cornes less than or more than 90 degrees. gmapping corrects these errors if the robot drives a second time through a corridor. But in the perfect case, Pico finds the exist by driving only onces through every corridor.
Slam not used
The maze information revealed that there will be no loops in the maze, and that the start end end of the maze will be on the boundaries of the maze. This meant that slam is not neccesairy to complete the maze while also making use of the arrows, so the maze can always be finished with the code that already was made. Due to the fact that it will take a lot of time compared to the results (solving the maze, which already could be done) it is decided not to implement slam.
Visualization
During the maze competition, rviz will be shown on a large screen. By using gmapping the maze solving process can be visualized. This visualization is split into two parts: visualization of the current target, and visualization of the followed path. In the next two sections both concepts will be explained and demonstrated by using the Gazebo simulation.
Visualize target
The ROS node Target sends every time step a new target over the topic /pico/target. A visualization node is listening to this topic to recieve the target. The build in Marker ROS display type is used to visualize the target. It is choosen to use a cylinder, because the target is send as a Point. The cylinder is placed at this point. Since the target is send as a point with respect to the frame /pico/base_link, the cylinder needs also to be placed with respect to this frame. Rviz performs the transformation of the /pico/base_link frame to the /map frame. The video below shows the result of this implementation.
Visualize path
To visualize the path taken by Pico, the locations of the pico in the past has to be remembered. It is choosen to remember only the position and not the orientation of Pico. The build in Marker Ros display type is used to visualize the path. To visualize the path, the line strip type is used. With this type, the points in the marker will be connecte with each other. The odometry information is used to receive the current location of Pico. The current point is added to the list of previous points. Therefore, when the new marker is publiced, the path is visualized from the start up to now. The marker is publiced in the /map frame to ensure that the stays at the same location in rviz. The video below shows the result of this implementation. As can be seen in this video, there is difference between the data received from the /pico/odom frame and publishing it at the /map frame. Transformation of the data from /pico/odom frame to the /map frame is not yet succesfully implemented.
Visualize path and target together
To visualize the path and the target together, the nodes described above can be run parallel at the same time. Only one has to take into consideration that the marker ID of the path is different from the market ID of the target. The video below shows the final result.
Results corridor competition
For the corridor competition, a step by step approach has been developed in order to steer the Pico robot into the (correct) corridor. Hereto, several subproblems have to be solved in a certain order as information of a subproblem is often needed to solve the next subproblem. The following subproblems can be distinguished:
- Corridor detection. With the aid of the various sensors of the Pico, the corridor has to be recognized, i.e. the corners of the corridor must be known.
- Path planning. By using the obtained information on the corridor, path planning can be used to guid the Pico into the corridor. Hereto, several way points are used.
- Drive. Destination points have to be translated into a radial and tangential speed, which can actually drive the Pico.
- Wall detection. For safety, an overruling program is needed which detects if the Pico is to close to any wall and if so can steer away from this wall.
These subproblems were implemented in three ROS nodes during: Target (corridor competition), Path (path planning) and Drive (drive and wall detection). This strategy resulted in a fast time of 26.8 seconds.
Results maze competition
During the maze competition, the software as described above was put to the test. After a rough start (the power connector was still attached), Pico successfully solved the maze in a fast time of 1 minutes, 4 seconds and 093 milliseconds. This time resulted in a second place.
During its journey through the maze, Pico successfully detected all dead ends and arrows, resulting in an optimal path through the maze.
At the first two corridors, we noticed that Pico wobbled just before the junction. We think that Pico went into safe drive mode at those points. Therefore, further fine tuning of the safe drive mode in combination with the used potentials could result in better results. Remarkable enough, this wobbling was not seen before the junctions with the arrows. Also, during our tests, we only encountered wobbling behaviour of Pico if the corridor was too small.
We had prepared some visualization in Rviz, since Rviz was shown during the corridor competition. During the maze competition, however, we were not recommended to use Rviz. We decided to listen to this advise and did not show the visualization in Rviz. Still, the intended visualization can be seen above during simulations in Gazebo.
Since other groups also have succesfully implemented our algorithms to solve the maze, even to get to first place, we are satisfied with the progress we made during this course.