Viotar/Hardware Design: Difference between revisions
No edit summary |
No edit summary |
||
| Line 86: | Line 86: | ||
==Estimation of the required motor power== | ==Estimation of the required motor power== | ||
Math test: | Math test: | ||
<math> | <math>1</math> | ||
<math>P=M_{T}</math> | <math>P=M_{T}</math> | ||
Revision as of 19:26, 26 November 2010
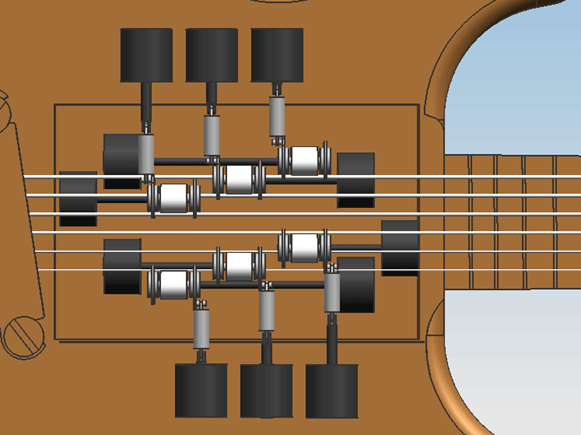
Design 0.1On friday the 5th of november, the first attempt at a design was finished. Only geometric constraints were taken into account, meaning the size of the engines and actuators were solely adjusted to the amount of space that was available in the guitar.
Design 0.2From reviewing design 0.1 with the group, the following points of improvement were determined:
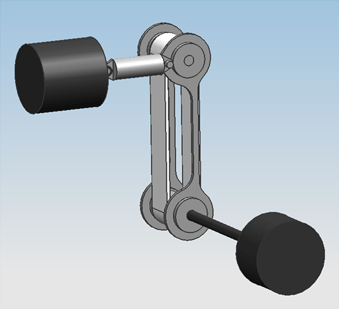
These improvements have been worked into design 0.2. Picking an actuatorIn the hardware design, six actuators are needed in order to push the bowing belt onto the string. These actuators have to be able to push with at least 4 Newton of force onto the belt. We also want the Viotar to be able to play 16 notes per second, so the actuator has to be fast two. After some research a hybrid linear actuator, made by Haydon, was found, a 21000 series size 8 linear actuator, to be precise. This actuator is not only very small, 21 mm square by 33 mm, but it is also powerful and fast enough to do the job. It can deliver up to 44 Newton of thrust and can travel at more than 50 mm/sec, depending on the thrust.
Estimation of the required motor powerMath test: [math]\displaystyle{ 1 }[/math] [math]\displaystyle{ P=M_{T} }[/math] The needed motor power is calculated using [math]\displaystyle{ P=M_{T}*\Omega }[/math]. For this, the total load [math]\displaystyle{ M_{T} }[/math] and the angular speed [math]\displaystyle{ \Omega }[/math] should be calculated. The total motor load consists of the load coming from the friction of the bowing belt with the string [math]\displaystyle{ M_{w} }[/math] and the friction of the bearing supporting the wheel that drives the belt, [math]\displaystyle{ M_{br} }[/math].
[math]\displaystyle{ M_{br} }[/math] is calculated assuming cylindrical roller bearings will be used. For cylindrical roller bearings [math]\displaystyle{ M_{br} }[/math] equals [math]\displaystyle{ F\mu_{w}d/2 }[/math], with [math]\displaystyle{ mu_{w}=0.002 }[/math] the friction coëfficient for cylindrical roller bearings, [math]\displaystyle{ F }[/math] the force on the bearing which is estimated at [math]\displaystyle{ 30 N }[/math], and [math]\displaystyle{ d }[/math] the shaft diameter, which is about [math]\displaystyle{ 4 mm }[/math] for a bearing with a outer diameter of [math]\displaystyle{ 11 mm }[/math].
|