User interface & General considerations: Difference between revisions
(Created page with 'The first step in modeling the motion planning algorithm with NetLogo consisted of creating the window with an adjustable dirt distribution that represents reality. The entire us…') |
No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
will adjust the amount of patches to the dimensions that are chosen. From a certain window size, | will adjust the amount of patches to the dimensions that are chosen. From a certain window size, | ||
the patch size is adjusted slightly to make sure that the whole window fits on the screen of the | the patch size is adjusted slightly to make sure that the whole window fits on the screen of the | ||
user of the model. | user of the model.<br/> | ||
[[File:Figure_2_interface.JPG|center|500px]]<br/> | |||
The above-mentioned dirt distribution is again modeled with the ideas as stated in Section 'The Window' | |||
At the start of each run of the model, each of the patches will receive a value of dirtiness between | |||
0 and 100 denoted with the variable dirt-level. The dirtiness value of patches is indicated | |||
by the color of the patches. The darker the color of the patch, the higher the dirtiness value of the patch. When a patch is completely clean, its color changes to blue. The earlier mentioned | |||
more or less even distribution of dirt will result in a random dirtiness value for all patches that | |||
lies between 10 and 30. Subsequently, a number of patch clusters, which can be specified with | |||
the nr-of-dirt-cluster slider, is selected from which the previously received dirtiness value is | |||
overwritten with a random number between 40 and 100. Additionally, there is a dirt-intensity | |||
slider included in the model. The value of this slider in % is divided by 100 and all the dirtiness | |||
values of the patches are multiplied by this number. So, when a patch would receive a dirtiness | |||
value of for instance 30 and the slider is at 50 %, the dirtiness value that the patch eventually | |||
receives is equal to 15. As has been stated earlier, all patches are assigned a number that denotes | |||
how hard it is to clean each of them. This number is obtained for each patch by taking | |||
a sample from an exponential distribution with mean 1 and multiplying this value by 100. Next, | |||
if the number is bigger than 1, it is set to 1. The resulting number is eventually stored in the | |||
variable hard_to_clean for each patch. When the robot moves over patches, its dirt-reduction | |||
will be multiplied with this number. Most of these patches will have a value for this number that | |||
is equal to 1, which has no effect on the dirt-reduction. A small number of patches will get a | |||
smaller number and are thus harder to clean. They thus require a lot more wiping motions to | |||
fully clean them. The just explained hard to clean possibility for patches can be turned on or off | |||
by means of a switch in the user interface denoted by hard_to_clean_active. Switching this | |||
off, results in a state that all patches have a hard-to-clean value of 1, which means that this | |||
variable has no effect anymore on the dirt-reduction of each patch. The dirt distribution is generated | |||
with the button Add Dirt. Re-clicking the button results in a newly generated dirt distribution.<br/><br/> | |||
As has been mentioned previously in Section 'Cleaning', the modeled window cleaning robot keeps | |||
track of the changes in dirtiness value of all patches. In the model this is done by storing not only | |||
the current dirtiness value of a patch in the variable dirt-level, but also storing the previous | |||
dirtiness value of a patch in the variable previous_dirt-level. The robot then compares the | |||
previous dirtiness value with the current dirtiness value when it moves over a particular patch with | |||
its cleaning section. When the reduction is smaller than a predefined standard, the patch is not | |||
considered by the robot anymore. This predefined standard is set with the min_dirtdecrease | |||
slider. The value of the slider is the minimum difference of the previous dirtiness value and the | |||
current dirtiness value for which the robot will still consider the patch as a patch that needs to be | |||
cleaned. The value of this slider is both used for the standard and the newly developed motion | |||
planning algorithms.<br/><br/> | |||
Apart from the already mentioned elements of the user interface, there are still a couple of buttons, | |||
monitors and one chooser that need to be explained. First, the Place Robot button places, as the | |||
name would suggest, the robot on the window. It however always places the robot in the middle | |||
of the window and not at a random position as has been stated earlier. This is done for a specific | |||
reason. When the robot starts cleaning the window, which is initiated with the Clean Window button, | |||
the robot first starts to move to the upper left corner for every programmed motion planning | |||
algorithm. The time that it takes to reach this top left corner is also added to the total cleaning | |||
time. To be able to compare the cleaning times of the considered motion planning algorithms with | |||
each other in an objective way, it is thus necessary that this time to reach the top left corner is | |||
always the same for all algorithms for a fixed window configuration. This is the reason for always | |||
placing the robot in the same position. Additionally, this is also the reason for not taking the time | |||
into account that the robot needs to turn at its initial place in the middle of the window to face the | |||
upper edge of the window. The robot is namely always placed with a random heading direction. | |||
To eliminate this source of randomness from the time that is necessary to move to the upper left | |||
corner, the initial rotation time is thus not considered.<br/><br/> | |||
Another choice in the model that was made in order to be able to make an objective comparison | |||
between the modeled algorithms was the choice for the implementation of the Import Window button. | |||
With this button, it is possible to import a previously used dirt distribution again. This option | |||
is necessary to test the considered motion planning algorithms on exactly the same conditions. It is a very welcome addition to the model, since there is a big factor of randomization included | |||
in the dirt distribution which can be eliminated in this way when that is deemed necessary. This | |||
button is also used to obtain the results presented in the Section 'Comparison'. To select a specific motion | |||
planning algorithm for testing, the chooser select_motion_planning is used. The option | |||
standard denotes the reference algorithm, zigzag denotes algorithm 1 and turndirt denotes algorithm 2 as described in 'algortithm 2'. The monitor time keeps track | |||
of the time that it takes the robot to clean the window. The monitors energy consumption and | |||
water consumption keep track of the energy consumption respectively the water consumption of | |||
the robot during the cleaning of the window. | |||
Latest revision as of 19:43, 2 April 2018
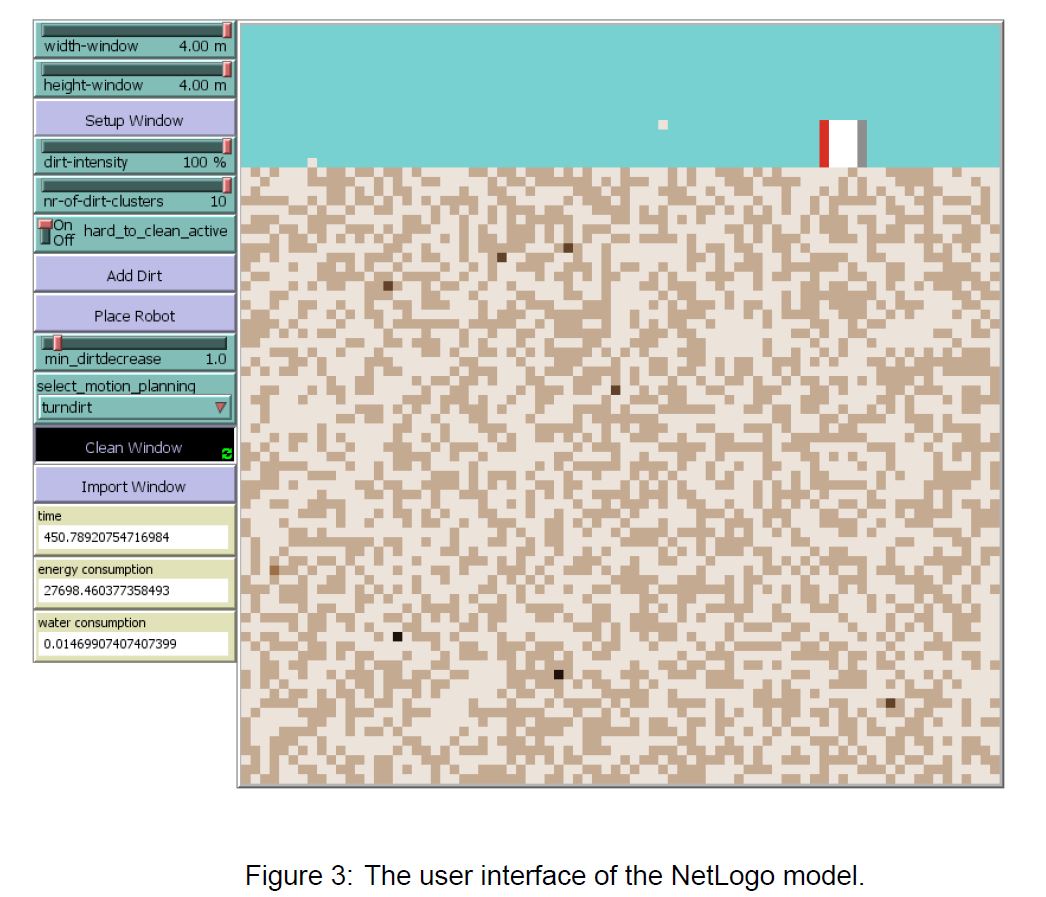
The first step in modeling the motion planning algorithm with NetLogo consisted of creating the
window with an adjustable dirt distribution that represents reality. The entire user interface including
the window and robot is shown in Figure 3 below. As mentioned before, a single patch from the
window represents an area of 50 x 50 mm. As can be seen in Figure 3, the dimensions of the
window can be adjusted by means of sliders. The width-window slider can be incremented with
250 mm which corresponds to 5 patches, while the height-window slider has an incrementation
of 250mmwhich corresponds to 5 patches. The reasons for these choices was already explained
in Section 'Design Choices'. When the sliders are moved, and the button Setup Window is pressed, the model
will adjust the amount of patches to the dimensions that are chosen. From a certain window size,
the patch size is adjusted slightly to make sure that the whole window fits on the screen of the
user of the model.
The above-mentioned dirt distribution is again modeled with the ideas as stated in Section 'The Window'
At the start of each run of the model, each of the patches will receive a value of dirtiness between
0 and 100 denoted with the variable dirt-level. The dirtiness value of patches is indicated
by the color of the patches. The darker the color of the patch, the higher the dirtiness value of the patch. When a patch is completely clean, its color changes to blue. The earlier mentioned
more or less even distribution of dirt will result in a random dirtiness value for all patches that
lies between 10 and 30. Subsequently, a number of patch clusters, which can be specified with
the nr-of-dirt-cluster slider, is selected from which the previously received dirtiness value is
overwritten with a random number between 40 and 100. Additionally, there is a dirt-intensity
slider included in the model. The value of this slider in % is divided by 100 and all the dirtiness
values of the patches are multiplied by this number. So, when a patch would receive a dirtiness
value of for instance 30 and the slider is at 50 %, the dirtiness value that the patch eventually
receives is equal to 15. As has been stated earlier, all patches are assigned a number that denotes
how hard it is to clean each of them. This number is obtained for each patch by taking
a sample from an exponential distribution with mean 1 and multiplying this value by 100. Next,
if the number is bigger than 1, it is set to 1. The resulting number is eventually stored in the
variable hard_to_clean for each patch. When the robot moves over patches, its dirt-reduction
will be multiplied with this number. Most of these patches will have a value for this number that
is equal to 1, which has no effect on the dirt-reduction. A small number of patches will get a
smaller number and are thus harder to clean. They thus require a lot more wiping motions to
fully clean them. The just explained hard to clean possibility for patches can be turned on or off
by means of a switch in the user interface denoted by hard_to_clean_active. Switching this
off, results in a state that all patches have a hard-to-clean value of 1, which means that this
variable has no effect anymore on the dirt-reduction of each patch. The dirt distribution is generated
with the button Add Dirt. Re-clicking the button results in a newly generated dirt distribution.
As has been mentioned previously in Section 'Cleaning', the modeled window cleaning robot keeps
track of the changes in dirtiness value of all patches. In the model this is done by storing not only
the current dirtiness value of a patch in the variable dirt-level, but also storing the previous
dirtiness value of a patch in the variable previous_dirt-level. The robot then compares the
previous dirtiness value with the current dirtiness value when it moves over a particular patch with
its cleaning section. When the reduction is smaller than a predefined standard, the patch is not
considered by the robot anymore. This predefined standard is set with the min_dirtdecrease
slider. The value of the slider is the minimum difference of the previous dirtiness value and the
current dirtiness value for which the robot will still consider the patch as a patch that needs to be
cleaned. The value of this slider is both used for the standard and the newly developed motion
planning algorithms.
Apart from the already mentioned elements of the user interface, there are still a couple of buttons,
monitors and one chooser that need to be explained. First, the Place Robot button places, as the
name would suggest, the robot on the window. It however always places the robot in the middle
of the window and not at a random position as has been stated earlier. This is done for a specific
reason. When the robot starts cleaning the window, which is initiated with the Clean Window button,
the robot first starts to move to the upper left corner for every programmed motion planning
algorithm. The time that it takes to reach this top left corner is also added to the total cleaning
time. To be able to compare the cleaning times of the considered motion planning algorithms with
each other in an objective way, it is thus necessary that this time to reach the top left corner is
always the same for all algorithms for a fixed window configuration. This is the reason for always
placing the robot in the same position. Additionally, this is also the reason for not taking the time
into account that the robot needs to turn at its initial place in the middle of the window to face the
upper edge of the window. The robot is namely always placed with a random heading direction.
To eliminate this source of randomness from the time that is necessary to move to the upper left
corner, the initial rotation time is thus not considered.
Another choice in the model that was made in order to be able to make an objective comparison
between the modeled algorithms was the choice for the implementation of the Import Window button.
With this button, it is possible to import a previously used dirt distribution again. This option
is necessary to test the considered motion planning algorithms on exactly the same conditions. It is a very welcome addition to the model, since there is a big factor of randomization included
in the dirt distribution which can be eliminated in this way when that is deemed necessary. This
button is also used to obtain the results presented in the Section 'Comparison'. To select a specific motion
planning algorithm for testing, the chooser select_motion_planning is used. The option
standard denotes the reference algorithm, zigzag denotes algorithm 1 and turndirt denotes algorithm 2 as described in 'algortithm 2'. The monitor time keeps track
of the time that it takes the robot to clean the window. The monitors energy consumption and
water consumption keep track of the energy consumption respectively the water consumption of
the robot during the cleaning of the window.