PRE2016 3 Groep13: Difference between revisions
No edit summary |
|||
| Line 212: | Line 212: | ||
<li> In this algorithm we must determine ourselves how much iteration rounds are needed and what the value for t is. </li> | <li> In this algorithm we must determine ourselves how much iteration rounds are needed and what the value for t is. </li> | ||
</ul> | </ul> | ||
== Further thoughts on the problem == | |||
Solving the problem in a ‘classical’ reinforcement learning way, would be defining actions like delaying cars (sending them away later) or sending cars over different roads, and then define a network which attaches probabilities to these actions. Then you train it with quite some situations, and then it develops a policy of probabilities of when to send cars. Basically it learns what to do with all the cars that want to leave. | |||
We want to use the NEAT algorithm, in the form of the NEAT-Python library. In very short terms, this algorithm evoluates a neural network with an evolutionary algorithm, and therefore you do not have to design such a neural network yourself. | |||
We want to find out how we can solve this reinforcemenat learning problem with NEAT-Python. | |||
== References == | == References == | ||
Revision as of 16:26, 8 March 2017
Introduction
This wiki page will display the possibilities of self learning navigational software. Throughout the report several points of attention will be introduced, investigated and processed in the prototype navigational system. The goal of the system is to create a cooperative/inter-vehicular, high-level (for example, no traffic lights) and based on the current situation (hardly any self driving cars, not all people have navigational systems). This research is set up trying to answer the following research question:
How can the travel time be minimized while maximizing overall utility, looking at user and society, by using a Self Learning, Inter-Vehicular Cooperative Navigation System (SLIVCNS)?
Problem description
Every day in the Netherlands people go to work with their cars, and every day the same thing happens, traffic jams causing a lot of pollution and waiting time. Most of the time people are traveling a lot longer than necessary to reach their goal. This gave us the idea to create a system that will reroute this traffic through secondary roads to minimize the overall waiting time or maybe even prevent traffic jams. By doing a lot of user research we hope to create a user friendly system that will help the user and society with this problem.
The simple problem
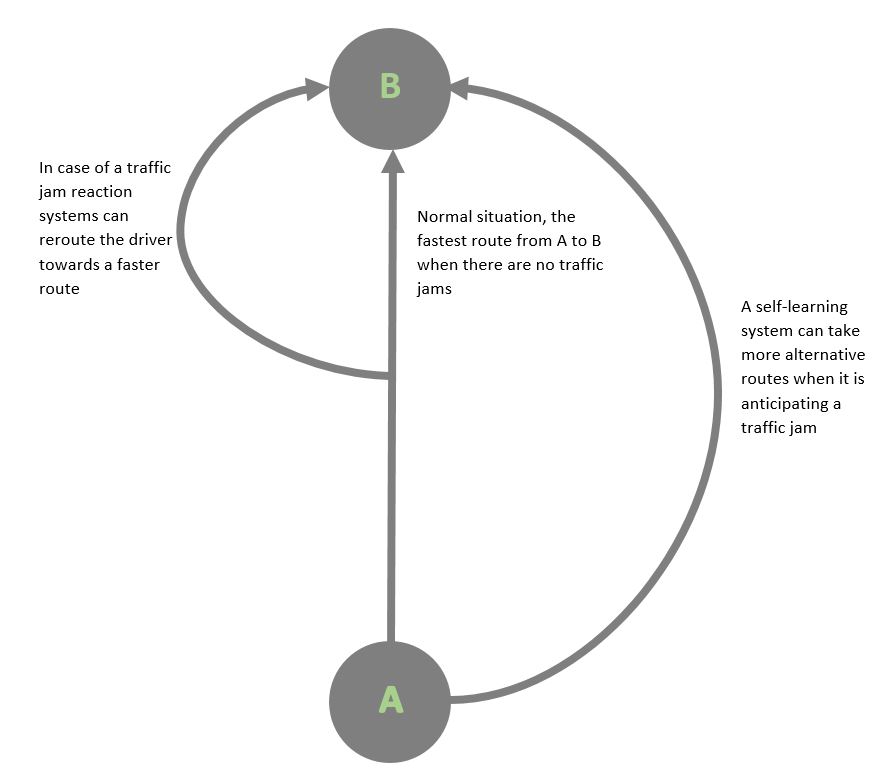
The problem in the simplest form is as follows, there is a city A and city B, in the morning people move from A to B to go to work. There is a highway (which is the fast route) and two secondary roads. When the people move from A to B a traffic jam occurs, this causes people to wait and increases their travel time. By rerouting a part of these people to the secondary roads this traffic jam can be minimized in such a way that two things can happen, or a mix of these: 1. The traffic jam is prevented and therefore the overall travel time is a lot lower, this is hard to implement as people who had to take the secondary road have longer travel time. 2. The traffic jam has become smaller and all the people whether they take the secondary road or the highway have the same travel time. This option seems more fair but still causes the problem of people waiting in traffic jams. Which one is to be preferred has to be researched as the user is very important in this decision.
The full problem
As seen above the problem can be made very simple but also a bit unrealistic, because in the end the system has to run in the real world, where there are thousands of ways to get from A to B. Also in the real world a lot of problems arise. Traffic is very unpredictable and can come from anywhere and go anywhere. It is not simply people moving from A to B. Also a lot of people will not be using our system, we will get no information from them, but they will have impact on our system. The biggest problem is all the unknowns, a lot of things can happen on the road. For example an accident can cause a traffic jam that can not be predicted. Because of all these problems we will be using self learning software to deal with these problems. This program will try to compensate for all the unknowns.
Objectives
Minimize travel time
The main goal of the system is to minimize travel time by rerouting users, to prevent longer waiting times caused by traffic jams.
Maximize overall utility
The utility can be split in three groups.
User
- Minimize travel time, this is the main objective as mentioned above.
- Estimate arrival time by predicting traffic jams so the user knows the optimal route and best moment of departure to reach the goal location on time.
- Making the system fair for all users. This will require user research in finding the fairest solution.
- Taking the privacy of the user into account by doing user research.
Society
- Traffic jam prevention to minimize unnecessary pollution, by rerouting to minimize unnecessary waiting time.
- Minimize disturbance by rerouting through less populated locations.
Enterprises
- Creating a system that is better than the present navigation systems, so potential users will be interested in buying this system.
State of the Art
There are a lot of different navigation devices available currently. The most simple one is only able to tell you the shortest route. A small upgrade also allows the user to exclude certain routes, like toll roads and tunnels. These often also give a choice for the user to either take a fastest (time) or shortest (distance) route. Some devices also allow traffic information incorporation which ask you to reroute if there is a traffic jam. When combining such a navigation system with a self driving car it is also possible to make the decision automatically. These all however respond to a situation instead trying to avoid certain situations.
Improvement over state of the art
To improve the state of the art it is important to know what the implications are of the current system. These systems will reroute users as soon as there is a faster route available and thus will distribute traffic equally over the roads available, which may seem like the optimal situation. A self learning system however should have more roads available, since it can predict traffic jams that haven't even happened yet. It can reroute the user many kilometers before the actual traffic jam and thus prevent new traffic jams in reroute roads.
Approach
The goal of the research is to improve the current traffic situation. This can only be considered an improvement when the changes do not diminish the overall utility. This means that within the navigation system the user as well as the society have to play an important role. As the time window is quite a tight one this research will be conducted simultaneously. The group of researchers will be split where four members of the team will work on making the self learning navigation work. The remaining two members will focus on the users and society. By frequent interaction, the team will be able to create a working navigational system in which the user and society will be strongly embedded. This also allows the prototype to be as representable as possible.
The completion of the program will also include a visual simulation which allows all team members as well as external personnel to use and understand the way the system operates, and what conclusions it provides.
User and Society
People behave differently when wearing something to hide their identity[1]. This also happens in a car. People are not directly visible and thus act more selfish. As long as people are driving their car (instead of autonomous), we can investigate further if/how we want to incorporate this.
Furthermore our navigation idea will request people to drive different roads, which at points will probably make them lose time on their journey. When looking at literature we find something called: “risk aversion”[2][3]. Risk aversion is a human trait where someone would avoid taking a favorable bet (overall travel time decrease) when it means they can directly lose out (more travel time)[4].
User research
To make sure all user preferences are taken into account a user research is conducted, focusing on the key aspects which should provide a strong basis for the product to be released to the public. The aim of the research, and thus leading factors into choosing the approach, is to gain as much information about as many different drivers as possible. Since the aspects of the research are predetermined, the best research method available is a questionnaire. Google Drive is used to host the questionnaire, because it has all features (sort of questions/ set-up) required for this research.
The link below will bring you to the questionnaire:
https://docs.google.com/forms/d/e/1FAIpQLScDPnmNoF6QXpMX930HC-V1ydxndn6kBt-_NZO-LiEaaBGuWA/viewform
The questionnaire is divided in several sections. Just like any research the questionnaire begins with a brief introduction of our idea followed by asking the participants permission to use the data they provide through an inform consent form. In all following sections the key issues are presented to possible users.
Section 1: Introduction questions
Section 2: Willingness to follow the system
Section 3: Fairness
The system can decrease travel time and traffic jams in several ways. The participants are presented with this way in a honest way. This means that we do present options where a user of the system is always equal or worse of to a person not using SLIVCNS. This sections is designed to get a better understanding of the target group, and to give a better insight into the goal our system should aim for.
Section 4: Privacy
The current state of the world means that almost all information gets shared. (insert link/reference) This however does not mean that all users all necessarily willing to share all information. Since our system needs to know certain things about users it is important to know that people do not mind sharing this information (anonymously). We ask the participants if they would be willing to share their current location as well as their destination. If the participant is willing to share this he/she is taking to the next section with follow-up questions. If the participant is not willing to share this information he is taken to the final stage of the questionnaire.
Section 5: System interaction
In this section the participants are asked to think about the idea of SLIVCNS, and how they would see such a system fit in their daily lives. It contains three subsections. The first subsection asks the participants what inputs they would like to have on the system. There are six predetermined options, like what type of roads, should the system take pollution into account etc. It is also possible to write your own input, if this is not present in the existing questions. The second question makes the participant think about how they would like to communicate with the system. As explained in Chapter %%%%%%%% it is important that the system knows when a user wants to travel from a to b. This means that a user would need to interact with the system quite frequently, which means that this interaction should be easy. Possible communications are for example a mobile app, an online website or a custom made interface. Once again the questionnaire provides room for a written answer. The final subsection is regarding the route planning of possible users. For the system to work optimally it is beneficial to know way in advance when users are going to drive. This section asks of different occasions (different destinations) the time a user would be able/willing to provide the system with its travel plans before departing.
Section 6: Finalizing questions
This section is focused on the aim of the navigational system. In this section the participants are asked about possible approaches the system could take regarding traffic/travel time distribution.
A participant is free to not answer a question if he/she does not want to answer, without having to provide an reason. All information helps towards optimizing SLIVCS for the user, and thus there are no mandatory questions (excluding accepting the inform consent form).
Low Level Implementation Ideas
Brick Algorithm
Introduction
We start by introducing a very easy model for our problem. It is not very expanded and therefore the model doesn’t really look like what will happen in the reality. In this model we only take into account the waiting time of driver (so no privacy, pollution, etcetera is taken into account ). Furthermore in this model we look at one part of the day: the morning rush and we will assume that everyone travels to the same destination. Our model is completely static and ironically it doesn’t take time into account. Moreover we assume that everyone uses our clever navigation system and that everyone is obedient to our clever navigation system and therefore they will always follow their directions.
Situation Representation
We will represent the current situation as a graph with vertices and edges, thus it will look like this:

The vertex that is two times circled is the destination, which means that the drivers from cities B, C and D have to go to this location (we don’t take drivers from city A into account, because they already arrived at their goal). The edges are driveways with a specific direction. So for each road there are two edges, because you can take the driveway forward or the driveway backward (for destination A however there are none driveway backwards, because if you are at destination A then you don’t have to drive back). Every driveway in this graph is indicated with a number and every city is indicated with a letter.
Data about roads and cities
We will assume that 30.000 people live in city B who all need to go to A. We will furthermore assume that 20.000 people live in city C, who all need to go to city A. Moreover we will assume that 10.000 people live in city D, who all need to go to city A. Last of all we will assume that the waiting time for each road is determined by a simple linear function: ax + b, where x is the amount of driver over a driveway (we will see later how x is determined), a is the capacity constant of the road (if it is lower then it can handle more drivers) and b is the constant, which indicated how much time drivers take minimal by taken a driveway. The result of this function is the amount of minutes that drivers have to wait before arriving at the new node. Now we have some more information about the roads:
- Roads 1 and 3 are huge highways (they can handle a lot of drivers), therefore they have the function 0.00025x + 15 (you need at least 15 minutes to drive over that certain road)
- Roads 2, 4, 5, 6 and 7 are little, short roads (In dutch: N-wegen) (and they can only handle a small amount of drivers) and these roads have the function 0.0005x + 5 (you need at least 5 minutes to driver over that certain road).
- Roads 8 en 9 are small, very short roads (you are soon at the new node by using this vertex) and have the function 0.0005x + 3 (you take at least 3 minutes to drive over that certain road).
How to determine x (amount of drivers over a certain road)
Driver can take different roads. Of course this will influence the value x. In this algorithm the value of x will start at 0, because at the start of our algorithm. Suppose we have some driver that live in city C, which drives over the driveways 6, 5 and 1 (in this order) and finally arrives at his destination A. If this happens then the x value for driveways 6, 5 and 1 is incremented by 1. Therefore the x value for driveways 6, 5 and 1 is now equal to 1. This is executed for all drivers, they keep driving over the driveways until they reach their final destination A and for every driveway we will increase the amount x by one if a new driver uses this driveway.
Comparing Solutions
Each way of driving must be comparable with each other way of driving (it must be a total order, so you must be able to say whether a < b, a > b or a = b). A value (cost value) is assigned to every solution (route drivers might take). The cost value that we use in our case is the sum of all waiting times for each driveway multiplied with the amount of drivers that take that certain road. So for example if 10.000 people have driven over road 1 and they have waited 17,5 minutes then the cost value for this road is 175.000, this will be summed with the cost values of all roads and then we will have our final cost value. A solution is better than another solution if it has a lower final cost value. Therefore our goal is to minimize the final cost value.
How will the drivers behave in optimal case?
That is something this artificial algorithm will determine (by assuming everyone will follow our clever navigation system). The main idea is that we will use a distribution table, where every driveway gets a certain value (tried by our artificial algorithm could be for example a gradient optimizer or a genetic algorithm). But how do drivers behave when all values are assigned. Suppose for example that driveway 1 gets a value of 20, driveway 4 gets a value of 40 and driveway 9 gets a value of 70 (those are all outgoing driveway from B) then this algorithm will say that (20/(20+40+70)) = (20/130) relative amount of all drivers from city B will take driveway 1, moreover (40/130) will take driveway 4 and last of (70/130) will take driveway 9. This will be done at the start of this algorithm for every city. Of course after this is done, not everyone has arrived at destination A. So we have to do this again and use the same distribution table. Hence city B has after the first “driving” round a new amount of drivers, which is equal to the amount of driver that went from city D to city B (by using driveway 5) added with the amount of drivers that went from city C to city B by using driveway 8. After this we will get a new “driving” round. This script will continue until everyone arrives at destination A.
What will happen if none or a few drivers to go city A?
We will limit our script till 10 “driving” rounds for example (you can take a different number than 10). If after 10 “driving” rounds not everyone has arrived at destination A then it will get a very high cost value (and therefore this is automatically a very bad solution, worse than solutions in which all drivers arrive at destination A). Our idea was for example to say that this value is equal to (Float_MaxValue) * (amount_drivers_at_start - amount_drivers_reached_destination) / (amount_drivers_at_start). This cost value has to be definitely higher than a cost value of a solution for which it is possible for everyone to arrive within 10 “driving” to destination A. If we define our cost value this way then a solution for which 10 “driving” rounds is too less to for everyone to get to their destination is worse than a solution in which everyone get to their destination in 10 “driving” rounds.
Advantages
- It is a very simple model, because it doesn’t need Neural Networks or other complex ways to find the solution. A gradient solver or genetic algorithm is enough to solve this problem.
- It can be easily expanded to multiple goals, where from each city they need to go to different nodes. Also for different times it can be used. Thus it will always find the best solution for every case, so it is complete and optimal.
Disadvantages
- Assumptions were made which are not very logical (waiting time is a linear function is not a very good assumption for example, likewise assuming that everyone will use our clever navigation system).
- For larger areas this algorithm will take a lot of time. Especially because this algorithm need to determine driveways * destinations * different_parts_of_the_day amount of constant. If you look for example at an area Germany and the Netherland then there is a huge amount of driveways and a huge amount of destinations. Hence you will have to determine a lot of constants.
- Because of the reason before this algorithm will also take a lot of memory for larger areas.
Matrix Algorithm
This is a way of optimizing to a very specific problem, with a given situation. It optimizes for that situation, so it will never be a real, general solution. It works by changing the input to something better, instead of learning how to convert any input to a certain solution.
Please remember that the problem solved here is mainly to get a feel for both the programming language and the type of problem. We know this problem is so simple you could easily solve it by other means, with much less effort, but that is a good way of checking our own results.
We assume there are two cities, A and B, and two roads from A to B. We assume cars leave in driving rounds, so in each round there is a certain amount of cars on the road. For example, a typical distribution of cars over one road would be [12, 3] which means that the first round 12 cars leave city A, and the second round 3 cars do so.
Of each road we know exactly how much time a car needs to travel the road given how much cars are on the road in total. This is a function which we will call the travel time function. We assume here it is of the form max(a * cars - b, min_travel_time), which means that up to a certain amount of cars on the road the travel time equals the minimum travel time needed to traverse the road, and above that the travel time increases linearly. The latter case is of course meant to signify a traffic jam.
One road is a highway, and the other road a secondary road which means that on the secondary road the minimal travel time is larger, a traffic jam occurs with less cars, and increases more per extra car. This is easily extendable with more roads, but for every road you would have to know this travel time function.
So for two roads together we have again a distribution matrix, for example [[8, 3], [3, 1]]. The idea is that we predetermine the amount of driving rounds, because changing the size of this matrix while optimizing is a bit of a problem still. (As a sidenote, in real life you would probably want to limit this because of user preferences anyway)
Optimizing the distribution matrix
We calculate the cost (travel time) of a certain distribution matrix by adding up the travel times of all the cars. This is the value that is going to be minimized. For the cars leaving the first round, the travel time for each car is given by the travel time function. For the cars in the second round, the same holds but we add the time that they had to wait while the first round was driving. We continue this for how many rounds there are. Then, if there are still cars left after all the rounds, we assume all these cars depart in the last round.
The program optimizes this matrix by minimizing the costs. Therefore, if there are sufficiently many rounds, no cars will be left behind, because if the number of rounds goes to infinity the cost of leaving cars behind will go to infinity as well.
The program
The program, written in Python with Tensorflow, has as input the matrix initialized with some values which should not matter too much. It then uses a Gradient Descent Optimizer to minimize the cost. The optimizer is run for a certain amount of steps with a certain learning rate, and then it outputs the optimized distribution matrix.
Drawbacks of this approach
- We have to predetermine the amount of driving rounds.
- We have to know for each road the travel time function.
- This generalizes and scales badly, because the matrix will get very large, and you need a matrix for every possible trajectory between two cities.
Problems with the current program
- It is very slow.
- When normalizing the distribution matrix values to a fraction of the total amount of cars instead, it should be more stable because it does not have to change values to whatever big amount of cars there may be so the learning rate can be smaller, but instead the results get very unstable.
- Currently when on the first round each cars take for example ten minutes to clear the road, the next round can depart after one minute if that is the minimal travel time. Changing this leads to unstable behaviour.
ILDB(+) Algorithm
Introduction
ILDB Algorithm stands for “Iterating Limited Distance Brick Algorithm”. This algorithm is an expanded version of the “Brick Algorithm”. Therefore it is really important to have read the “Brick Algorithm” and understand how it works. This algorithm is an improve of the “Brick Algorithm” because it also work for a more larger scale. The idea of this algorithm is based on that traffic jams only occur at local scale, which means that if a lot of traffic has to go to Eindhoven then the traffic jams occur close to Eindhoven.
Situation Representation
We are trying again to see the problem as a graph with nodes and vertices, likewise the “Brick Algorithm”. However this time the graph is more complex (to illustrate the difference between the “Brick Algorithm” and this algorithm):
In this example A, G and J are goals. And to make the situation less complex we will assume that cities with subscript A have 2000 humans that need to go to A. If a city doesn’t have subscript A then 200 humans need to go to A from that city. For subscript G and J the same holds. Furthermore we assume that every black road has 1 lane and has a minimal time of 10 minutes. Every orange road has 2 lanes and has a minimal time of 20 minutes. And every green road has 3 lanes and has a minimal time of 30 minutes. Then we also have red road, which has a minimal time of 15 minutes and has 1 lane.
Calculation Waiting Time
The calculation of the waiting time for roads is the same as the Auction House algorithm.
How does the algorithm works?
In the “Bricks Algorithm” you have different driving rounds. In this algorithm you get some new type of round called iteration round. We first take a look at a certain radius from every goal by only looking at minimal time and we take 30 minutes for example. So every node that is in t minutes of a goal is taken into account. We take t is 30 minutes in this example and you might notice that every city that has a subscript of that certain goal is within 30 minutes of that goal. Then we start with the first iteration round:
First iteration round
In the first iteration round you will use the “Brick Algorithm” for every goal separately and for everyone that has to go to his goal and is within t minimal waiting time from its goal. You will discard every node in this example that is further than t time from its goal and every road that goes to a discarded node or comes from a discarded node is also discarded. So in this example you will use the “Brick Algorithm” for three zones with subscript: A, G and J (note that zones doesn’t have to be disjunctive) and you will found the optimal solution for these zones. After that (same iteration round) you will take back the discarded nodes and vertices and take a look at humans that will travel to a goal and are outside of that zone (so for example someone from a city that hasn’t got subscript A wants to travel to A). In this case you will use the shortest path algorithm to that certain zone taken into account the new waiting time due to the traffic jams that drivers within a zone have created. If travelers from outside the zone enter the zone with their shortest path algorithm, they will use the “Brick Algorithm” to get to their destination.
Other iteration rounds
The second iteration round is executed after the first iteration round is executed for every goal zone and the second iteration round will check where the drivers from outside the zone have entered the zone in the first iteration round and will take them into account as new inhabitants of that node that have to go to that certain goal for the “Brick Algorithm”. So suppose 500 outsiders have entered zone J by going to H, then in the “Brick Algorithm” drivers that have to go from H to J is increased by 500. After this a third iteration round is executed and will take the results of the second iteration round into account etc. This iteration is stopped after u iteration rounds have passed where we will determine u based on the calculation time of this algorithm.
What if two goals are close to each other?
This algorithm calculate separately for each goal what the optimal local solution is, however if two goals are close to each other then it will not take the other goal into account, which might be bad. Therefore you might say that when you calculate the local solution for a certain goal that you also take other goals within a radius of 2*t into account, so you will use the “Brick Algorithm” for multiple goals at the same time. Then you discard the result of the other goals and you will use only the result of the goal that you were calculating. This algorithm will be called “ILDB+ Algorithm”.
Defense of Assumption
The ILDB Algorithm is based on the assumption that traffic jams for traffic going to a certain location only occur close to that location. This assumption is very logical, because if for example there is some event going in Amsterdam and a lot of drivers from Berlin go to Amsterdam then no traffic jam will occur in Germany because of the drivers that will go to Amsterdam (traffic jams in Germany might happen, but they have a different cause).
Advantages
- It can also solve the problem for larger problems more efficiently than the “Brick Algorithm”.
- It needs less memory than the “Brick Algorithm” to solve the problem.
- It doesn’t need Neural Networks or other complex ways to find the solution. A gradient solver or genetic algorithm is enough to solve this problem.
Disadvantages
- It is harder to see if this algorithm is complete and always find the most optimal solution than for the “Brick Algorithm”, because a lot of path distributions are discarded in this solution.
- If the assumption that traffic jams going to a certain location only occur close to that location is a very wrong assumption, then this algorithm doesn’t work (if it is partially true then this algorithm might still work).
- This algorithm is more complex than the “Brick Algorithm” and therefore harder to understand and implement.
- In this algorithm we must determine ourselves how much iteration rounds are needed and what the value for t is.
Further thoughts on the problem
Solving the problem in a ‘classical’ reinforcement learning way, would be defining actions like delaying cars (sending them away later) or sending cars over different roads, and then define a network which attaches probabilities to these actions. Then you train it with quite some situations, and then it develops a policy of probabilities of when to send cars. Basically it learns what to do with all the cars that want to leave.
We want to use the NEAT algorithm, in the form of the NEAT-Python library. In very short terms, this algorithm evoluates a neural network with an evolutionary algorithm, and therefore you do not have to design such a neural network yourself.
We want to find out how we can solve this reinforcemenat learning problem with NEAT-Python.
References
[1]https://newrepublic.com/article/117152/how-sunglasses-and-masks-affect-moral-behavior
[2]http://www.jstor.org/stable/2937956?seq=1#page_scan_tab_contents