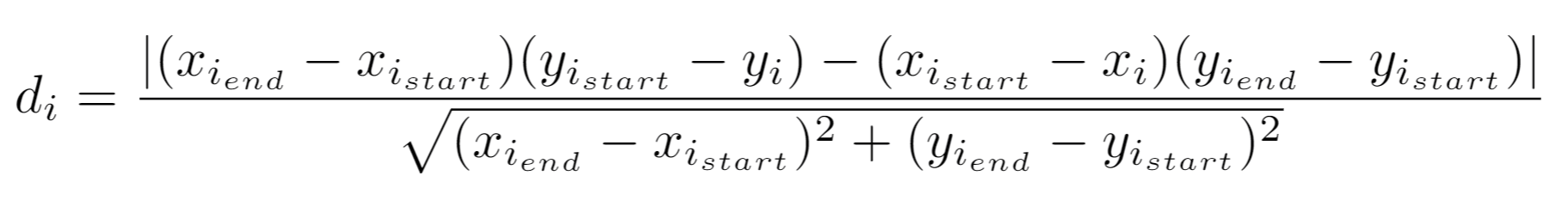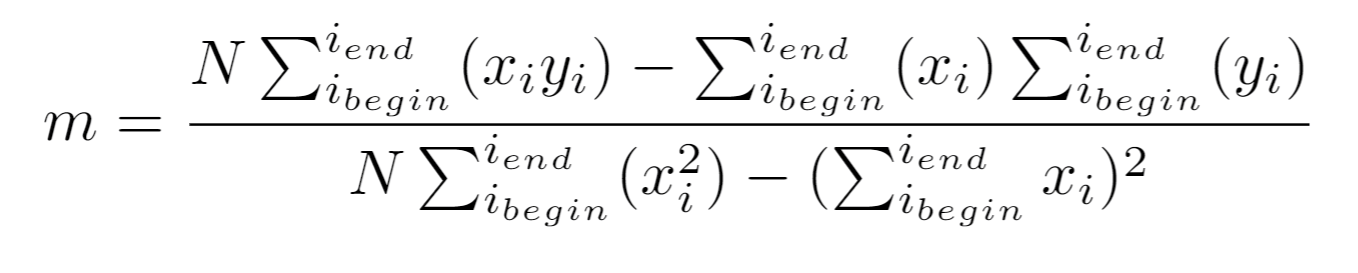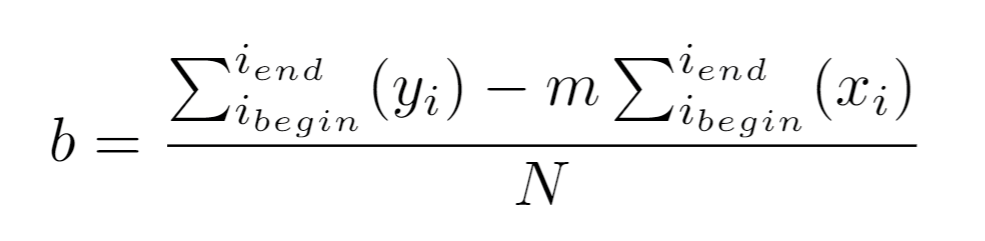Mobile Robot Control 2021 Group 6: Difference between revisions
| (51 intermediate revisions by 2 users not shown) | |||
| Line 30: | Line 30: | ||
==Line | ==Line Extraction Algorithm== | ||
Line detection from data points is a fundamental task in many fields of science and engineering. In the case of the mobile robot, line detection algorithm is the underlying cornerstone for feature extraction, such as wall, corner and entrance detection. | Line detection from data points is a fundamental task in many fields of science and engineering. In the case of the mobile robot, line detection algorithm is the underlying cornerstone for feature extraction, such as wall, corner and entrance detection. Moreover, by using lines as features that consist only of two points, the amount of data to be processed for corner and entrance detection is reduced. This improves computational effort. | ||
===Pre-processing of Laser Data=== | |||
[[File:Pico_coordinates.png|300 px|thumb|right|Figure 1: The coordinate system used with the angular limits of the LRF.]] | |||
PICO acquires its data points via the laser range finder (LRF). The LRF outputs in one sweep 1000 data points, consisting of the distances (<math>r</math>) corresponding to particular angles (<math>\theta</math>), as shown in Figure 1. The first data point is at -2 rad and the last data point is at +2 rad. Invalid data points above 10 m and below 0.01 m are filtered out. The data points are then converted from polar coordinates to cartesian coordinates using the following geometric relations: | PICO acquires its data points via the laser range finder (LRF). The LRF outputs in one sweep 1000 data points, consisting of the distances (<math>r</math>) corresponding to particular angles (<math>\theta</math>), as shown in Figure 1. The first data point is at -2 rad and the last data point is at +2 rad. Invalid data points above 10 m and below 0.01 m are filtered out. The data points are then converted from polar coordinates to cartesian coordinates using the following geometric relations: | ||
[[File:X coordinate.PNG|200 px|]], | |||
and | and | ||
[[File:Y coordinate.PNG|200 px|]], | |||
where i is the index starting from 0 and ending at 999. <math>\Delta \theta</math> is the angular resolution, which is 4 mrad. | |||
===Segmentation=== | |||
The line segmentation algorithm is based on the iterative end-point fit (IEPF) algorithm. The algorithm works as follows: | [[File:Line segmentation algorithm.PNG|400 px|thumb|left|Figure 2: The line segmentation algorithm [1].]] | ||
The line segmentation algorithm is based on the iterative end-point fit (IEPF) algorithm [1]. The algorithm is illustrated in Figure 2 and works as follows: | |||
1. A line is first drawn from the first data point (i_begin) to the last data point (i_end). This corresponds to -2 rad and +2 rad respectively when all data is valid, i.e. not filtered out. | 1. A line is first drawn from the first data point (i_begin) to the last data point (i_end). This corresponds to -2 rad and +2 rad respectively when all data is valid, i.e. not filtered out. | ||
2. The perpendicular distances from the line are calculated for each data point between i_begin and i_end. | 2. The perpendicular distances from the line are calculated for each data point between i_begin and i_end [2]: | ||
[[File:Perpendicular distance.PNG|500 px|]]. | |||
3. The line is split at the point with the largest perpendicular distance from the line if it is above a certain threshold. | 3. The line is split at the point with the largest perpendicular distance from the line if it is above a certain threshold. | ||
4. If it is below the threshold, a line is found and the segment is stored. The algorithm goes back to | 4. If it is below the threshold, a line is found and the segment is stored. The algorithm goes back to step 2, but sets i_begin equal to one index further from the end of the last segment found. If it is not below the threshold, it goes back to step 3 and splits the line again. | ||
5. The algorithm repeats until all data points are considered, i.e. i_begin is now at i_end. | |||
6. Lines consisting only of a few data points are thrown away. These lines are considered not reliable. | |||
[[File: | This is also called the split-and-merge algorithm, but merging is not done. The drawback of omitting the merging part is that the threshold in step 3 has to be large enough in order to prevent multiple lines from being detected due to noise in a single wall. Increasing the threshold may result in incorrectly indentifying a line between a wall and a small wall segment, e.g. a thin protruded wall. For the escape-room this is fine, because there are no such protruding walls. However, if there are thin protruding walls in the hospital challenge, a merging algorithm has to be implemented too. A merging criterion based on the chi-squared test is considered, which determines the difference between two lines based on their combined covariance matrices [3]. | ||
===Line Fitting=== | |||
After a new segment has been found, a line is fitted through the laserdata points of this segment. This makes the line less prone to noise influences. The line is fitted via the linear least-square method by calculating the slope m and intercept b: | |||
[[File:Linear least square.PNG|300 px|]], | |||
[[File:Linear least square b.PNG|300 px|]]. | |||
However, the disadvantage of using the linear least-square approach is that it can not represent lines parallel to the y-axis. This is due to <math>\Delta x</math> becoming 0, which causes the slope m of the line to approach infinity. This is solved practically by only applying the linear least-square method when the distance x between the begin point and end point of the line is above a certain threshold. Because of the limitation of the linear least-square approach, a total least-square solution is considered for the Hospital challenge, which overcomes these limitations. | |||
==Entrance Detection== | ==Entrance Detection== | ||
| Line 69: | Line 88: | ||
If there are more segments located, it will iterate through each segment and compares its slope with the following 2 segments. If there are 2 segments located, the algorithm will check if the system is parallel. If so, the system detects it as a hallway. Based on if a hallway is detected or an interance, a entrance point is calculated between the lines. | If there are more segments located, it will iterate through each segment and compares its slope with the following 2 segments. If there are 2 segments located, the algorithm will check if the system is parallel. If so, the system detects it as a hallway. Based on if a hallway is detected or an interance, a entrance point is calculated between the lines. | ||
[[File:Ezgif.com-gif-maker.gif]] | |||
= Hospital Competition = | = Hospital Competition = | ||
| Line 99: | Line 118: | ||
|- | |- | ||
|} | |} | ||
=Bibliography= | |||
[1] http://ais.informatik.uni-freiburg.de/teaching/ss09/robotics/slides/feature_extraction.pdf | |||
[2] Tomáš Kubín, Martin Čapek, Jiri Stastny - Simple Distance Line-point Algorithm for Line Extraction from 2D Laser Data - Mendel University in Brno | |||
[3] Samuel T. Pfister, Stergios I. Roumeliotis, Joel W. Burdick - Weighted Line Fitting Algorithms for Mobile Robot Map Building and Efficient Data Representation - California Institute of Technology | |||
Latest revision as of 23:04, 6 June 2021
Group Members
Stefan van der Palen - 1501054
Paul Munns - 1522795
Saray Bakker - 1002248
Liang Oei - 1522779
Boudewijn Kempers - 1398164
Walter MacAulay - 1632817
Design Document
The Design Document: media:MRC_Design_Document_Group6.pdf
Escape Room Competition
For the Escape room competition two version were build, a smarter robot and a back-up version were the robot follows the wall. For both cases a 20 Hz execution rate is used.
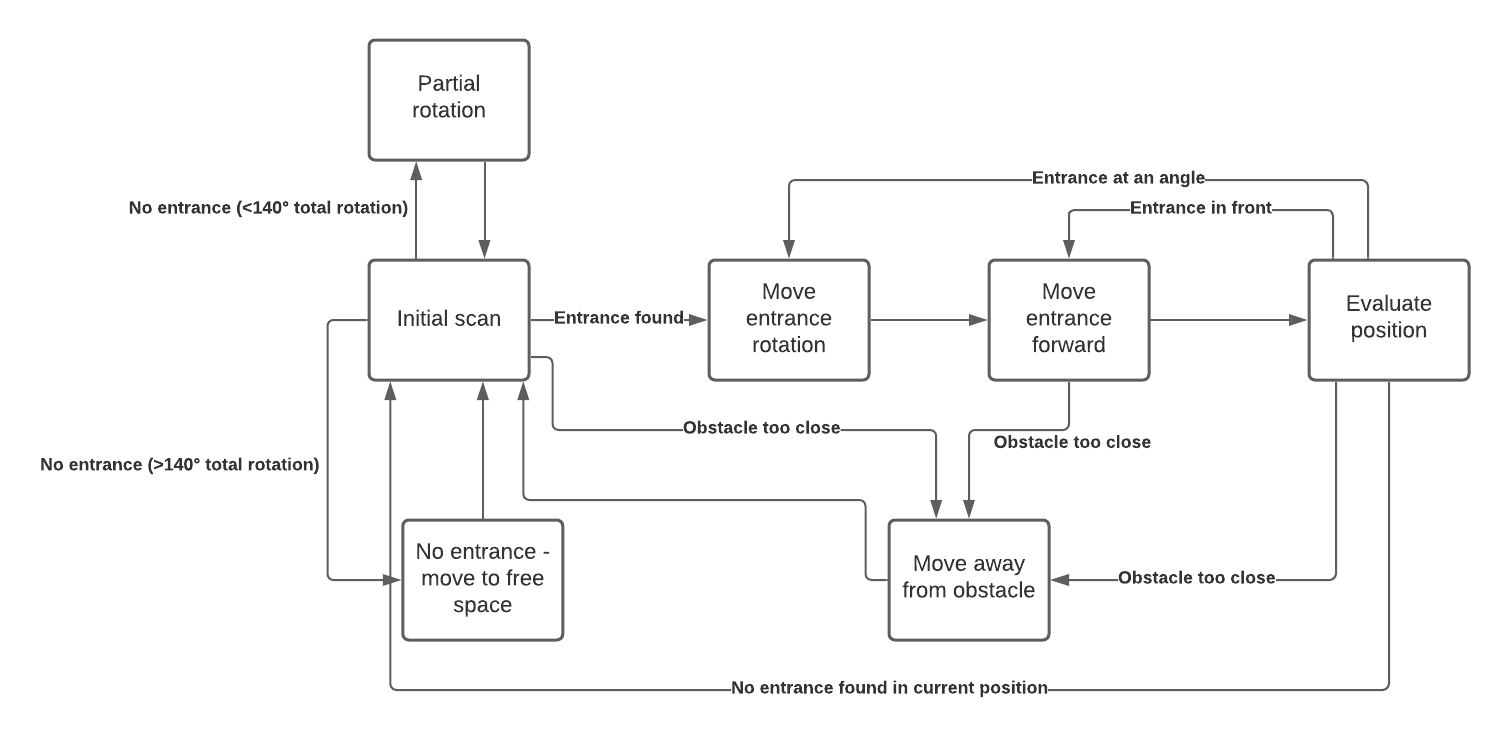
The general structure of the smarter robot is given below. First, an initial scan is performed to find the entrance of the hallway. If an entrance is found, PICO will receive a point where it can move towards via the states 'Move entrance rotation' and 'Move entrance forward'. How the exit is determined is explained in the section 'Line segments and entrance detection'. If no entrance is detected, PICO will perform a partial rotation of 30 degrees and start scanning again for an exit. When no entrance is found after performing a full scan of the room, it is likely that the entrance is not visible from the current position of the robot. In the state 'No entrance - move to free space', PICO will move forward towards a new spot and try to locate the entrance at the new position.
If an entrance is detected, PICO will rotate until it faces the entrance and move forward. Since it should be taken into account that PICO might indicate an exit where there is none, an evaluation is performed after a few steps. If the entrance is still in front of the robot, PICO keeps moving forward. If the entrance is not directly in front of PICO due to drift, a rotation is performed before moving forward again. It could be possible that a false exit was detected before or PICO has drifted too much to still find the exit. Then a new full room scan is performed.
PICO should avoid running into obstacles including static and dynamic objects. Therefore a function is designed that maintains a certain distance from all obstacles which is called 'bubbleRobot'. When PICO is too close to an obstacle, it will stop and move in the opposite direction. To avoid running into the obstacle again, the movement away from the obstacle is more than the distance to leave the bubble. When the robot has moved away from the obstacle, it will reevaluate its position.
Line Extraction Algorithm
Line detection from data points is a fundamental task in many fields of science and engineering. In the case of the mobile robot, line detection algorithm is the underlying cornerstone for feature extraction, such as wall, corner and entrance detection. Moreover, by using lines as features that consist only of two points, the amount of data to be processed for corner and entrance detection is reduced. This improves computational effort.
Pre-processing of Laser Data
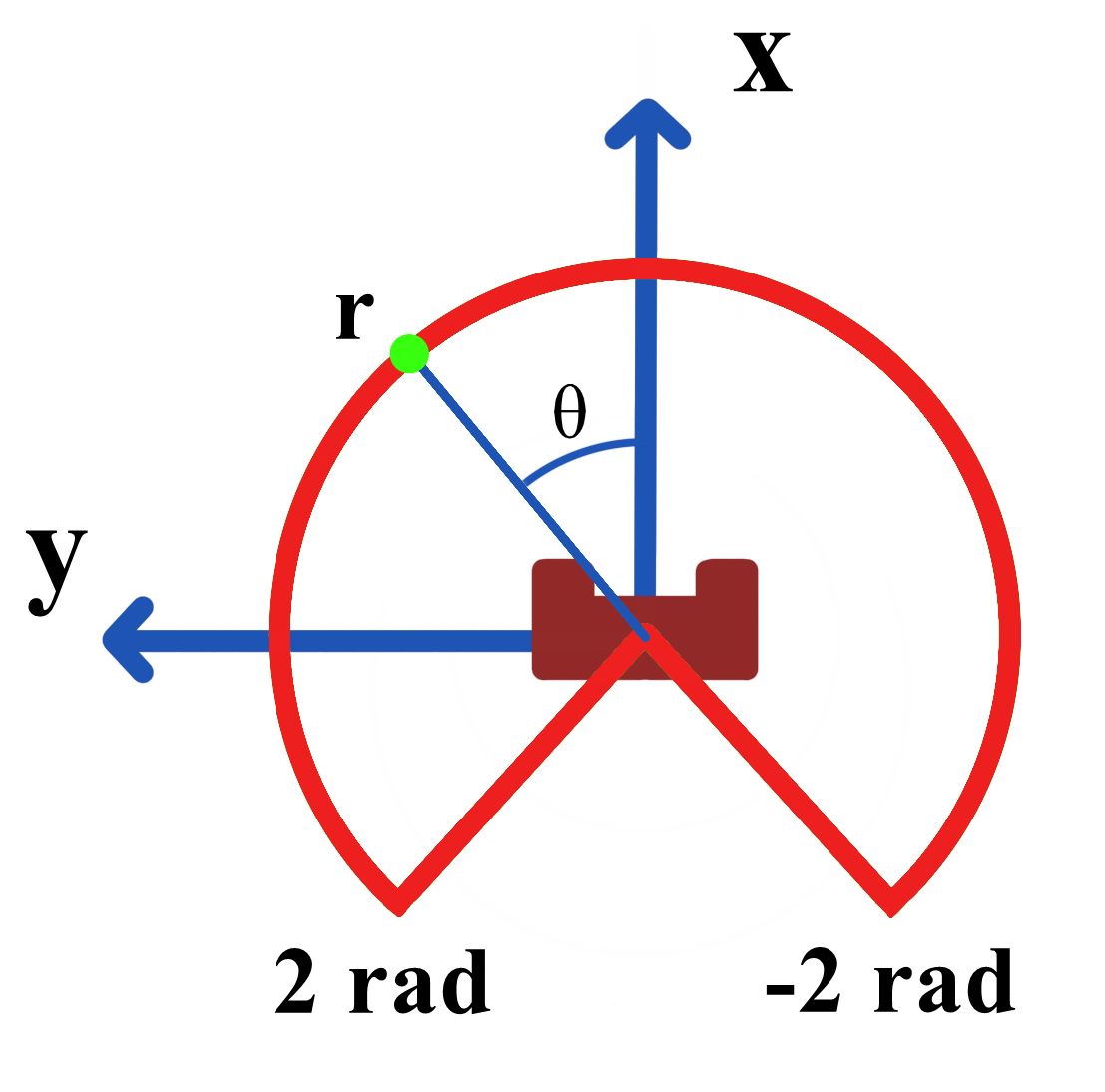
PICO acquires its data points via the laser range finder (LRF). The LRF outputs in one sweep 1000 data points, consisting of the distances ([math]\displaystyle{ r }[/math]) corresponding to particular angles ([math]\displaystyle{ \theta }[/math]), as shown in Figure 1. The first data point is at -2 rad and the last data point is at +2 rad. Invalid data points above 10 m and below 0.01 m are filtered out. The data points are then converted from polar coordinates to cartesian coordinates using the following geometric relations:
and
where i is the index starting from 0 and ending at 999. [math]\displaystyle{ \Delta \theta }[/math] is the angular resolution, which is 4 mrad.
Segmentation
The line segmentation algorithm is based on the iterative end-point fit (IEPF) algorithm [1]. The algorithm is illustrated in Figure 2 and works as follows:
1. A line is first drawn from the first data point (i_begin) to the last data point (i_end). This corresponds to -2 rad and +2 rad respectively when all data is valid, i.e. not filtered out.
2. The perpendicular distances from the line are calculated for each data point between i_begin and i_end [2]:
3. The line is split at the point with the largest perpendicular distance from the line if it is above a certain threshold.
4. If it is below the threshold, a line is found and the segment is stored. The algorithm goes back to step 2, but sets i_begin equal to one index further from the end of the last segment found. If it is not below the threshold, it goes back to step 3 and splits the line again.
5. The algorithm repeats until all data points are considered, i.e. i_begin is now at i_end.
6. Lines consisting only of a few data points are thrown away. These lines are considered not reliable.
This is also called the split-and-merge algorithm, but merging is not done. The drawback of omitting the merging part is that the threshold in step 3 has to be large enough in order to prevent multiple lines from being detected due to noise in a single wall. Increasing the threshold may result in incorrectly indentifying a line between a wall and a small wall segment, e.g. a thin protruded wall. For the escape-room this is fine, because there are no such protruding walls. However, if there are thin protruding walls in the hospital challenge, a merging algorithm has to be implemented too. A merging criterion based on the chi-squared test is considered, which determines the difference between two lines based on their combined covariance matrices [3].
Line Fitting
After a new segment has been found, a line is fitted through the laserdata points of this segment. This makes the line less prone to noise influences. The line is fitted via the linear least-square method by calculating the slope m and intercept b:
However, the disadvantage of using the linear least-square approach is that it can not represent lines parallel to the y-axis. This is due to [math]\displaystyle{ \Delta x }[/math] becoming 0, which causes the slope m of the line to approach infinity. This is solved practically by only applying the linear least-square method when the distance x between the begin point and end point of the line is above a certain threshold. Because of the limitation of the linear least-square approach, a total least-square solution is considered for the Hospital challenge, which overcomes these limitations.
Entrance Detection
Laser data can be quite noisy, which can result in a false detection of the entrance when just using one scan as input. Therefore a few scans after each other are performed. The median of the estimated angle and distance towards the entrance is used to plan the motion.
The entrance detection algorithm uses the slopes of the walls to detect the entrance. Firstly the walls are detected via line segmentation of which the slopes can be calculated. For each segment (wall), the slope is compared to the slope of wall that follows next and also the slope of the wall that follows the next wall. So in total 3 segments are used for the algorithm. The following are compared; - The slopes are compared to each other if they are parallel/perpendicular in a certain bound. These bounds are introduced since the walls can be not perfectly parallel or perpedicular. These bounds also determine the robustness of the algorithm. - If the end-point of a segment is in a certain bound of the begin-point of the next segment. If these points differ a lot, this most likely will be an entrance and an entrance point is calculated.
If there are more segments located, it will iterate through each segment and compares its slope with the following 2 segments. If there are 2 segments located, the algorithm will check if the system is parallel. If so, the system detects it as a hallway. Based on if a hallway is detected or an interance, a entrance point is calculated between the lines.
Hospital Competition
Meeting Schedule
| Date | Chairman | Secretary | Summary |
|---|---|---|---|
| 26-4-2021 | - | - | Introduction meeting |
| 28-4-2021 | Boudewijn Kempers | Paul Munns | First tutor meeting, dividing tasks for Design document |
| 3-5-2021 | Boudewijn Kempers | Paul Munns | Divide coding tasks: Perception (Liang and Paul), Path planning (Saray and Stefan), Initial/Main (Boudewijn and Walter) |
| 10-5-2021 | Paul Munns | Stefan van der Palen | Show functionality of wall following robot (dumb robot), show status smart robot which uses perception to find the entrance. |
| 17-5-2021 | Stefan van der Palen | Walter MacAulay | .. |
| 26-5-2021 | Walter MacAulay | Saray Bakker | .. |
| 31-5-2021 | Saray Bakker | Boudewijn Kempers | .. |
| 7-6-2021 | Boudewijn Kempers | Paul Munns | .. |
Bibliography
[1] http://ais.informatik.uni-freiburg.de/teaching/ss09/robotics/slides/feature_extraction.pdf
[2] Tomáš Kubín, Martin Čapek, Jiri Stastny - Simple Distance Line-point Algorithm for Line Extraction from 2D Laser Data - Mendel University in Brno
[3] Samuel T. Pfister, Stergios I. Roumeliotis, Joel W. Burdick - Weighted Line Fitting Algorithms for Mobile Robot Map Building and Efficient Data Representation - California Institute of Technology