Group2 19-1 Week6
Notulen tutor meeting
- Afweging om aan oppervlakte te blijven/ naar de bodem, duidelijker beschrijven. Zijn ‘luxe-positie’ dingen,
- Deel onder navigation verduidelijken,
- Parts list verder uitwerken, staat nog veel ‘stuff’ op
- Als we experimenten 2x (of meer) willen uitvoeren, moeten sommige instrumenten ook meerdere keren mee
- Welke experimenten willen we waar doen?
- (comsol evt. gebruiken voor temperatuur modellen)
- Kan de power source een beperking zijn voor de kwaliteit van de experimenten?
- Necessary bandwidth, eigenlijk een methode nodig om uit te rekenen. Wat nu gebruikt wordt is niet echt een valid argument. Daarnaast zijn bijv. cameras al beter geworden.
- Uitrekenen hoeveel data je uit welk experiment krijgt, en dit met hoe lang de missie duurt.
- Willen we ons experiment nog uitvoeren? Dan langs Harry van de stikstof
- Movement under water kan wel uitgebreider. Wat is de aandrijver en wat zit er tussen de nucleaire bron en de propulsion?
- Does it work at high pressure?
- Uitzoeken hoe electromotor onder water zou kunnen werken
- Ballast water naar binnen stromen en eruit pompen kost ook veel energie, berekenen hoeveel de submarine in totaal gebruikt
- Extraterrestrial life - precautionary principle opzoeken
- Het onderzoek gaat steeds meer in op of de missie wel kan, hier op anticiperen
- Autonomie
Week 6 Logbook: Overall
 To allow navigation up and down, it is most convenient if the submarine will stay afloat at rest. For this, it should have a density equal to that of water. But water, although it has a low compressibility, is not entirely incompressible. As Fine and Millero showed, the specific volume of water decreases (and thus the density increases) as the external pressure increases. [1] Due to this fluctuation in density, the buoyant force on the submarine will increase as the submarine goes deeper down (where the pressure is higher). Hence, if the submarine floats at crust level, it will be pushed up.
From the data of Fine and Millero, a pressure dependency of the density of water can be derived: =1004.79*e3.20629*10-5p With ρ the density in kg/m^3 and p the pressure in bar.
(The observant reader may note that at p=0 Pa, the density of water is 1004.79 kg/m^3, rather than 1000. That is due to the fact that an increase in temperature accompanying the increase in depth was taken into account. The first data point is at 16 MPa, 0 degrees Celsius. Supposing you could then decrease the pressure on the water, the function assumes that you are also decreasing the temperature, which results in a density increase. However, as the pressure in Europa’s ocean won’t decrease below 16 MPa, the function works just fine in the relevant regime.)
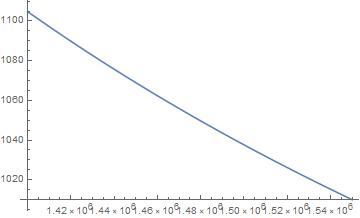
The figure below shows ρ(p(r)); the density of the water in Europa’s ocean between the seafloor and the sub-crust surface.
Ideally, the submarine itself has a density a little over 1100 kg/m^3, making it sink. However, if the submarine carries a kind of balloon filled with a material X with the following properties:
X has a lower density than water
X has a higher compressibility than water.
What ideally happens is that the submarine is attached to the balloon. Their total mass is m. The volume of the submarine is V0, the balloon’s is V(p), so that the density of the combination is =m/(V0+V(p)). V(p) is inversely proportional to the pressure, so as the pressure increases, V(p) decreases, so the density goes up. If this decrease in V(p) can be made to occur in such a way that the average density of the combination is at all times equal to the density of the water it is floating in.
Let’s illustrate this with an example. Suppose the submarine has a mass of 750 kg, and a volume of .5 m^3. The balloon has a mass of 50 kg. The density of the combination is then:
=800/(0.5+V(p))=1004.79*e3.20629*10-5p, Where the last equality follows from the density of water. Rewriting this equation results in a formula for V(p): V(p)=0.7962*e-3.20629*10-5p-0.5 Filling in a few particular values gives V(1)=.2962 m^3, V(160)=.2921 m^3, V(3000)=.22317 m^3.
The density of X as function of pressure then becomes: (p)=50/(0.7962*e-3.20629*10-5p-0.5)
An idea for materials with the required densities can be acquired here. The accurate value of the density of suitable materials can then be found in literature. (Such as oxygen: https://www-sciencedirect-com.dianus.libr.tue.nl/science/article/pii/0378437177900826)
To allow navigation up and down, it is most convenient if the submarine will stay afloat at rest. For this, it should have a density equal to that of water. But water, although it has a low compressibility, is not entirely incompressible. As Fine and Millero showed, the specific volume of water decreases (and thus the density increases) as the external pressure increases. [1] Due to this fluctuation in density, the buoyant force on the submarine will increase as the submarine goes deeper down (where the pressure is higher). Hence, if the submarine floats at crust level, it will be pushed up.
From the data of Fine and Millero, a pressure dependency of the density of water can be derived: =1004.79*e3.20629*10-5p With ρ the density in kg/m^3 and p the pressure in bar.
(The observant reader may note that at p=0 Pa, the density of water is 1004.79 kg/m^3, rather than 1000. That is due to the fact that an increase in temperature accompanying the increase in depth was taken into account. The first data point is at 16 MPa, 0 degrees Celsius. Supposing you could then decrease the pressure on the water, the function assumes that you are also decreasing the temperature, which results in a density increase. However, as the pressure in Europa’s ocean won’t decrease below 16 MPa, the function works just fine in the relevant regime.)
The figure below shows ρ(p(r)); the density of the water in Europa’s ocean between the seafloor and the sub-crust surface.
Ideally, the submarine itself has a density a little over 1100 kg/m^3, making it sink. However, if the submarine carries a kind of balloon filled with a material X with the following properties:
X has a lower density than water
X has a higher compressibility than water.
What ideally happens is that the submarine is attached to the balloon. Their total mass is m. The volume of the submarine is V0, the balloon’s is V(p), so that the density of the combination is =m/(V0+V(p)). V(p) is inversely proportional to the pressure, so as the pressure increases, V(p) decreases, so the density goes up. If this decrease in V(p) can be made to occur in such a way that the average density of the combination is at all times equal to the density of the water it is floating in.
Let’s illustrate this with an example. Suppose the submarine has a mass of 750 kg, and a volume of .5 m^3. The balloon has a mass of 50 kg. The density of the combination is then:
=800/(0.5+V(p))=1004.79*e3.20629*10-5p, Where the last equality follows from the density of water. Rewriting this equation results in a formula for V(p): V(p)=0.7962*e-3.20629*10-5p-0.5 Filling in a few particular values gives V(1)=.2962 m^3, V(160)=.2921 m^3, V(3000)=.22317 m^3.
The density of X as function of pressure then becomes: (p)=50/(0.7962*e-3.20629*10-5p-0.5)
An idea for materials with the required densities can be acquired here. The accurate value of the density of suitable materials can then be found in literature. (Such as oxygen: https://www-sciencedirect-com.dianus.libr.tue.nl/science/article/pii/0378437177900826)