Embedded Motion Control 2014 Group 10
Members of group 10
| Bas Houben | 0651942 |
| Marouschka Majoor | 0660462 |
| Eric de Mooij | 0734166 |
| Nico de Mooij | 0716343 |
Planning
Week 1
- Introduction
- Install Ubuntu
Week 2
- Determine the course goals
- Brainstorm about the robot control architecture
- Start with the tutorials
Week 3
- Continue with the tutorials
- Install ROS/QT
- Finish robot control architecture
- Brainstorm about collision principle
- Brainstorm about navigation
Week 4
- Meet with the tutor
- Finish installation
- Finish tutorials
- Write collision detection
- Write corridor navigation
- Test the written code on Pico
- Corridor challenge (Recorded performance)
Week 5
- Meet with tutor
- Software structure designed
- Started working on the scripts
Week 6
- Meet with tutor
- Software structure design rejected and redesigned
- First target point/dijkstra based algorithm
- Pico experiment
Week 7
- Meet with tutor
- Target point changer added
- Artificial blind spots added to the algorithm
- Arrow detection algorithm designed
- Experiment
Week 8
- Prepare final presentation
- Final presentations
- Start/Finish detection added
- Double check for deadlock added
- First version of Arrow detection added
- Pico experiment
Week 9
- Meet with tutor
- Final version of Arrow detection added
- Arrow detection tested on multiple cases with different red patterns in it.
- Pico experiment
- Maze competition (Recorded performanceAttempt I, Recorded performanceAttempt II)
Week 10
- Finish wiki
Corridor competition concepts
Collision avoidance
Since we had some difficulties with installing linux and gazebo, we started working on the corridor code relatively late. Therefore, we opted for a basic collision detection algorithm, using one detection area at pico's left and one at pico's right. Both areas range from 0.15m to 0.3m, and check angles in a range of 135 degrees. The collision avoidance system is dormant until an object enters one of these detection area's. Once this happens, pico will turn to the other side, while simultaneously performing a sideways motion away from the obstacle. During this process, pico continues to drive forward. To guarantee that pico does not collide with any objects, we implemented an extra collision detection range. Once an object enters the range of 0.25m at any angle, pico will stop driving forward. The angular and longitudinal corrections, however, will stay active. The different collision ranges are displayed in the image below.
In this picture, the red area indicates the inner collision detection circle, and the yellow and blue area's represent the left an right side detection area's, respectively.
Even though the collision avoidance code used during the corridor competition is very robust for avoiding collisions, it induces a saw-tooth like motion, which is obviously sub optimal. It did, however, prove to be sufficient for the corridor competition.
Intersection detection
Similarly to the collision avoidance, we opted for a temporary, basic solution for corridor detection. The easiest way to detect corridors is to check for the absence of walls in a certain angle increment. With an angle increment of α radians, a gap in the wall is detected as a corridor if its width exceeds α times the distance between pico and said wall. Since our collision avoidance does not guarantee a set distance to the wall, we deemed this corridor detection system inappropriate for accurate corridor detection.
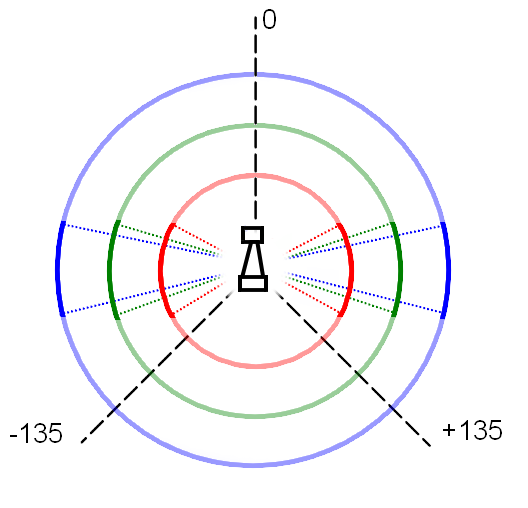
To prevent the minimum corridor width from scaling with the distance between pico and the wall, we check for the absence of walls in 3 areas per side of pico. The area's have angle increments of 74 degree's, 36 degrees and 24 degrees, with radii of 0.5m, 1.0m and 1.5m, respectively. These detection ranges are displayed in the image below.
In this image, the red, green and blue circles are the inner, middle and outer detection radii, respectively, and the dotted lines represent the angles increments. Please note that this picture is drawn with an arbitrary scale.
For a gap in a wall to be detected as corridor, all three detection ranges must be free of laser data points. This means that corridors of over 0.6m wide will always be detected, and corridors of under 0.3m in width will always be ignored. The exact distance between the wall and pico will determine whether corridors with a width between 0.3m and 0.6m are detected as corridor. Gaps of this size, however, should not exist in the corridor challenge.
Concepts
Robot program architecture
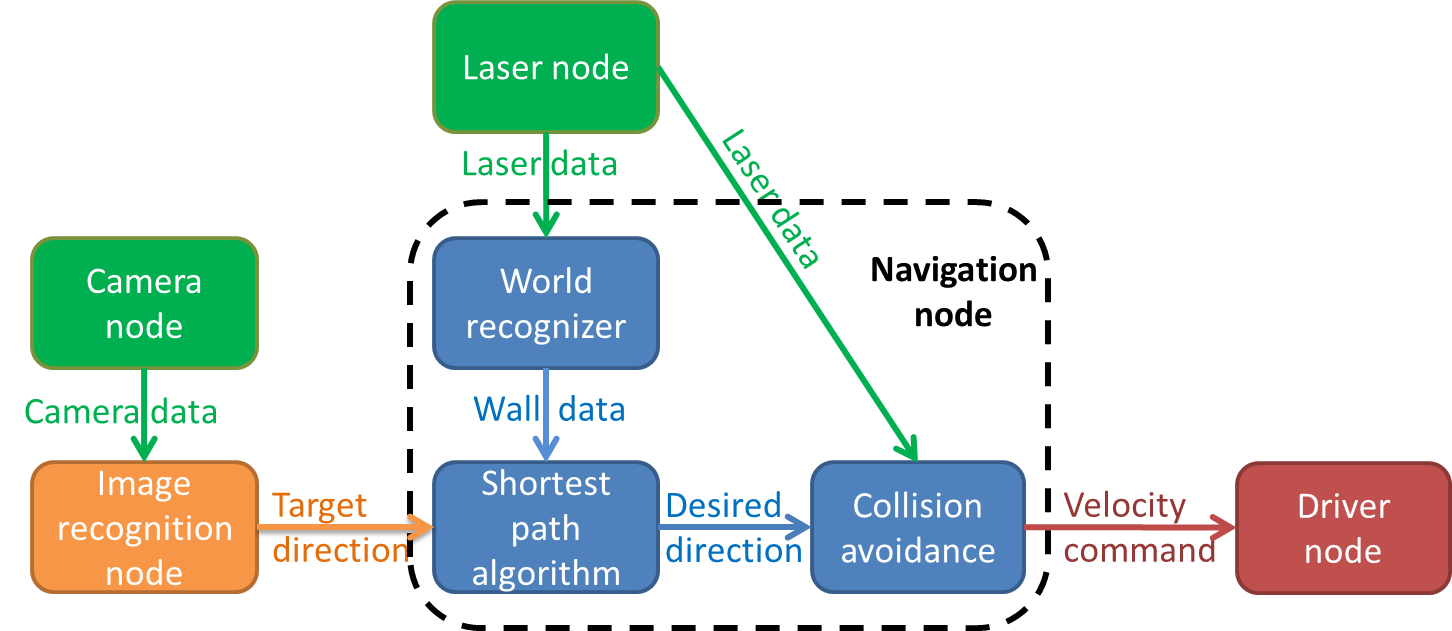
Even though the initial idea was to give every distinguishable function its own node, several main functions were placed together in one node, because they have to communicate large matrices with each other.
Besides the laser, camera and drive node's provided for the course, two additional nodes were added: the image recognition node and the navigation node. All main functions and their interactions can be seen in the figure below.
The program runs three consecutive main steps, listed below.
Determining strategy
In the first step, pico determines what strategy to apply, depending on whether an arrow is detected or not. The default strategy is to follow the wall to the right, executed by taking every right turn available. From now on, this method will be called the 'right hand rule'. When an arrow is detected in the distance, the strategy is changed to driving straight forward, towards the arrow. If the arrow is close enough to take the turn, the strategy is set to either the right hand rule or left hand rule, according to the direction of the arrow. When no arrow is detected, the strategy will return to the default right hand rule. This step involves the 'Camera node' and the 'Image recognition node', which will be explained in more detail later. The 'Camera node' sends camera data to the 'Image recognition node', which then searches for an arrow. The image recognition node provides a target direction for the second step, according to any arrows it might recognize.
Path finding
In the second step, the strategy determined by step one will be executed with the aid of Dijkstra's shortest path algorithm. This algorithm detects whether a turn is available, and whether it has a dead end or not. It then calculates an optimal path according to the turn options available. This step involves the 'Laser node' and the 'World recognizer" and 'Shortest path algorithm' functions of the 'navigation node'. These two functions will be explained in further detail later on. The 'Laser node' sends laser data to the 'World recognizer' function, which makes a map of the walls currently visible, and stores it in a matrix. The 'Shortest path algorithm' function uses this matrix to determine an optimal path. This optimal path is converted to a desired direction vector, which is used in the third step.
Collision avoidance
In the third step, the desired direction vector provided by the previous step is checked for collisions, and altered accordingly. This involves the 'Laser node' and the 'Collision avoidance' function of the 'Navigation node'. The 'Laser node' provides the 'Collision avoidance' function with laser data. This data is used to determine if any walls come within a certain safety range. When this occurs, the desired direction provided by the previous step is altered to avoid collisions. If no collisions are imminent, the desired direction is left unaltered. The possibly altered desired direction is transformed to a velocity command, which is then send to the 'Driver node'.
World recognizer
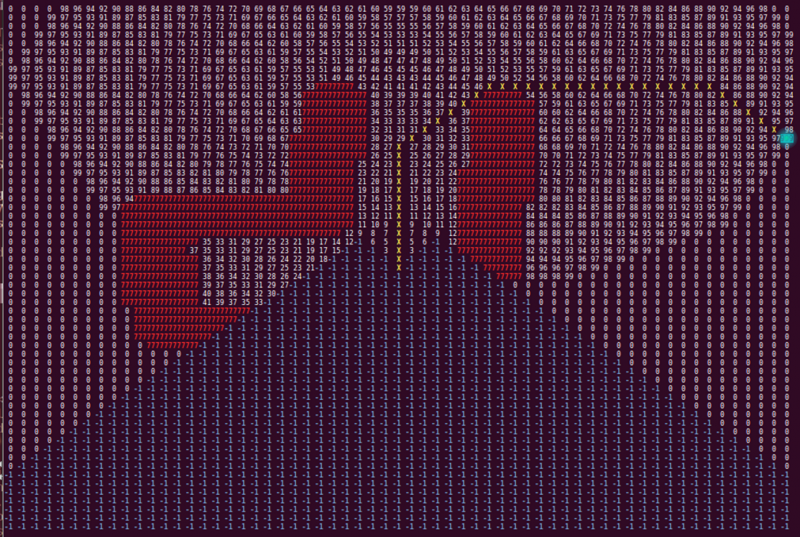
The 'World recognizer' function converts the laser data provided by the 'Laser node' to a matrix used in the 'Shortest path algorithm' function. This matrix contains all areas pico is not allowed to go. The matrix represents a square grid around pico. The amount of cells and cell size are determined before hand. A zero in the matrix means that the respective cell is unoccupied. Each point of the laser data array is transformed to a position in the grid, and every cell in a safety circle with a diameter of 5 cells around this point is marked as occupied. Walls get the number 777 assigned to their cells. Assigning walls with a distinct number allows for easier human reading and coloring options. The safety circle is added to maintain a distance between the walls and the optimal path, and to ignore small gaps as possible corridors. In the picture below, an example of the matrix with detected walls is shown.
The walls are represented by the blue line's which are dotted for walls outside pico's vision range. The occupied matrix cells are depicted by the number 777, colored red. The 0 with the green rectangle is the position of pico. As can be seen, angle's of 90 degree are not depicted as such, which can be caused by inaccurate laser data, scaling errors, or inaccuracies in the laser range detectors specifications. However, slight curving of walls does not in navigational errors, and is thus of little importance.
To prevent pico from driving to his blind spot, all non visible cells are marked as occupied, this time with the number -1. Again, a distinct number for each kind of occupation allows for easier reading and coloring of the matrix. The physical blind spot is expanded by a region on each side, to prevent pico from turning back into the corridor he came from. These artificial blind spots have the added benefit of initiating a deadlock when pico is driving head first into a wall. How this deadlock works is explained in the section about the optimal path algorithm. In the image below, the matrix is shown with blind spots.
Again, the red numbers 777 indicate that a grid is occupied by a wall, and the 0 with green rectangle is pico's position. In addition, each blue -1 represents a cell in the blind spot. The highlighted area in the blind spot is pico's natural blind spot and the non highlighted areas are the artificial blind spots.
Shortest path algorithm
The matrix provided by the 'World recognizer' function is used in the 'Shortest path algorithm' function to determine the optimal path with the use of a modified version of Dijkstra's algorithm. The algorithm starts at pico's position, and looks if the adjacent cells, including diagonal ones, are occupied. In the grid matrix, every adjacent cell with a zero will be occupied, changing the zero for a cost number. The cost number is dependent on how long the path it belongs to is. The shortest path available, thus with the lowest cost number, is the first to be expanded. A horizontal or vertical move adds a cost of two, and a diagonal move a cost of 3. The expansion of paths is looped until the target point is encountered. The target point is represented by a 999 in the matrix, and is placed either above pico, to the right and slightly above, or to the left and slightly above, depending on which target direction has been received from the 'Image recognition node'. In the image below, a the matrix containing the walls and blind spots is depicted after the path finding algorithm.
In this image, the red 777's are again the walls, the blue -1's are the blind spots, the 999 is the target point, in this case for the right hand rule, and the white numbers are the pathing costs. The yellow crosses represent the optimal path.
The pathing algorithm has some additional features. The most important one is the already mentioned deadlock. When no optimal path can be found for two consecutive iterations, pico initializes a 90 degree turn in the opposite direction of the target point. This does also occur when pico gets stuck. Furthermore, the walls are inflated, as mentioned before, which means that small gaps are not seen as corridors. The path finding algorithm runs twice per second, and outputs a desired direction vector, which is the vector describing the distance between the 5th pathing point and the first pathing point, which is located at pico's position. This point should represent the direction pico should drive to follow the beginning of the path. The fifth point is chosen because it is a compromise between the advantages of the first few points and points further down the path. Points close by have a very large angle increments, for example 45 degrees for the second layer. Points further down the path run the risk of ending up at the other side of walls, in case the path wraps around a wall. Since walls are at least 5 cells wide, this is not possible with the 5th point.
Collision avoidance
The "Collision avoidance' function checks the desired direction, provided by the 'Shortest path algorithm' function, for collisions and, if necessary, alters the desired direction. To check for collisions, pico checks the laser data array for the closest laser data point. If this point is within 0.38m of pico, a correction vector is created, pointing away from said closest point. The closer this point is to pico, the larger the correction vector. The desired direction vector and correction vector are then added together to obtain the final direction vector, which is then scaled to 0.2m/s. This mechanism acts like a one way p controller. In the picture below, the principle of the collision avoidance is illustrated.
In this picture, pico is represented by the blue dot,the range of 0.38m is represented by the blue dotted circle, and the red rectangle represents the wall. The green arrow depicts the desired direction vector, the red arrow is the correction vector and the black arrow is the final direction. Please note that this image has objects with arbitrary size, and are thus not scaled properly.
Arrow Detection
In order to detect arrows and determine its direction, a roadmap is designed. The first couple of steps is applied to all evaluated frames, but the second part is conditional. Before analysis is possible, all considered data (ROS RGB) is converted to the OpenCV format. This converted data then is converted to a HSV image.
With the use of a threshold, the red pixels are filtered out of the HSV image. The data is put in a binary image in which the originally red parts are white and the different colored surroundings black. Because red can be found in both the left and right side of the HSV color spectrum, two different thresholds were required.
After acquiring the frayed binary image it is blurred and then the floodfill algorithm is applied. Using a kernel of size 3x3 results in sufficiently smoothened contours. Now all contours are saved in a contour vector and colored differently. The data now is formatted to an analyzable form.
The analysis start with calculating the area of each different contour. The index of the largest contour is stored and the closest rectangle available is drawn around the corresponding contour. If this largest area contains less pixels than a set minimum, the data is said to not contain an arrow and the algorithm restarts by loading the next considered set of data received from the camera. If the largest area however contains more pixels the analysis continues with the next step. This threshold makes sure not every contour is considered in the analysis, but also prevents the possibility to detect an arrow from a large distance.
After passing the first test, the rectangle is divided in two equal parts by using the base coordinates of the rectangle. In both the right and left part of the rectangle the amount of dots is counted. The amount-of-dots-ratio then is determined and should be at least 1.5 in order for the contour to be an arrow. If this isn’t the case, the algorithm restarts in the same way as stated before. When passing this condition the white area in the rectangle is considered. The original HSV data now is thresheld for the filtering out the white parts. The earlier mentioned largest contour then is used again in order to specify the amount of white dots around the arrow. If there are sufficient white pixels, an arrow is detected. The navigation target then is set to driving straight forward. When the arrow however contains more than a certain amount of dots, the navigation target is said towards the direction of the arrow (using the amount of dots in the two regions of interest).
Algorithm testcase
In order to test the previously prescribed algorithm, the following images are used as testcase.
These figures are edited printscreens from a recorded bagfile. Further finetuning of the parameters testing the scrips and communication is done using bagfiles.
Additional features
A couple of additional functions, not worth their own block in the diagram, have been implemented.
Entrance detection
When the code starts to run, pico's target point is set in the upper middle of the matrix. Once pico encounters walls behind his y axis, or a certain time has passed, the target point is set to the default position. This is done to prevent pico from driving in circles outside the maze.
Exit detection
Once pico encounters no walls within two meters in a angle of 90 degrees to the front, his target point is set to the upper middle of the matrix, prompting pico to drive straight forward. Once there are no walls within 2 meters in pico's vision range, the maze is completed, and pico commences a victory dance.
Decoupling of translations and rotations
To prevent pico from standing still while turning, we completely decoupled rotating from driving. Translations will not be delayed until pico faces the right direction, but are instead executed sideways if needed. Meanwhile, pico will start to turn towards the direction he is driving. The big advantage of this feature is that, excluding deadlocks, pico will never stand still. The largest disadvantage of this feature is that pico can not prevent collisions when driving backwards. However, by adding the artificial blindspots, we disabled pico's ability to drive backwards, essentially nullifying the disadvantage of decoupling rotations from translations.
Victory dance
Once pico has left the maze, the robot initializes a victory dance. We consider the maze as solved when no walls can be found within 1.5m in any direction. Once this condition is fulfilled, pico will start moving its right, quickly followed by a movement to his left. Thereafter, pico moves right again, back to the position where the dance started, and turns 90 degrees around. After that, the dancing steps are repeated until the end of time. Obviously, the victory dance has no function in its current form, but finding a open spot might be useful for other kinds of robots.
Encountered problems
Corridor code
While programming the corridor code, few problems were encountered. Aside from several compilation errors, the simulations went without any problems. However, the experiments prior to the corridor competition did pose several difficulties. The rotational velocity in gazebo is limited at 0.5 rad/s, but the actual robot did not have such a limitation. Since the rotational velocity in the script was way higher than 0.5 rad/s, the collision detection was over-tuned, resulting in a saw-tooth like path. Additionally, the 90 degree turn was incorrect as well, due to the rotational velocity of over 0.5 rad/s. Both problems were solved by properly re-tuning the rotational velocity constant.
Dijkstra's algorithm
As is common with computations as complicated as Dijkstra's shortest path algorithm, several compilation errors were encountered in this part of the code. These were solved by standard compilation error solving techniques. Aside from these compilation errors, several functionality bugs had to be solved. The first bug was caused by improper matrix sizes, resulting in 'segmentation faults'. By expanding both the path storage and cost function matrices, these problems seemed to be solved. In certain cases, however, the segmentation faults continued to exist. This turned out to be caused by not programming the boundaries of the grid, and thus the storage matrix, in the algorithm. By implementing these boundaries, several strange numbers in the grid matrix disappeared as well. The boundaries for the walls have been set at the 2nd layer, keeping the outer layer unoccupied. This allows the algorithm to go around walls that reach to the edge of the grid, preventing unnecessary deadlocks. After this change, the algorithm functioned properly. However, the desired results were not yet obtained. Pico could drive backwards, if that was shorter, and often turned back into the corridor he just left.
To let our pathing algorithm work as intended, we had to apply some modifications to Dijkstra's algorithm. First, we added the blind spot of pico, and modeled it as a solid wall. This solved the problem of driving backwards. However, pico could still turn back in corridors he had just left. Our first idea to prevent this, was adding a short term map memory. By letting walls remain in the algorithm for a few seconds after disappearing from pico's sight, we would have solved pico's tendency to turn back into corridors, while simultaneously preventing pico from displaying indecisive behavior at moments that walls disappear from the grid. However, short term wall memory turned out to be very hard to implement. With pico driving around and turning simultaneously, the position of old walls had to be corrected often and accurately. Because we did not know the exact position of the laser range finder relative to pico's rotational axis, we did not manage to apply the proper coordinate transformations to the wall. Furthermore, wall memory proved to be extremely susceptible to ghost points, whose harmful effects were amplified by the inflation of the walls in the grid. All these factors combined prompted us to look for alternative solutions.
Our next idea was to block of the old entrance with artificial blind spots. While relatively simple, this idea proved to be surprisingly effective. After some tuning of the blindspots shape, we solved both the indecisive behavior and pico's tendency to turn back into the corridor he just left. While the artificial blindspots often completely block old corridors and out of sigh walls, this is not required for proper navigation. The shape of the blindspots reduce pico's possible drive directions to a 90 degree angle in front of him. Combined with the rotational speed of 0.5 rad/s, pico can not make infinitely small corners, but has a minimum corner range of about 0.4m. Therefore, turning back into the corridor pico just left is physically impossible without stopping or driving forward for some time. Since both possibilities do not occur without a deadlock or detected exit, we can guarantee that pico will never turn back into corridors unintentionally. After this change, our pathing algorithm worked as intended.
Target point
The pathing algorithm requires a target point to work, which is dependent on the maze solving strategy currently active. The target point for driving straight forward is easy: in the middle of the most upper row. For the right hand strategy, however, the choice is less intuitive. Originally, we placed the target point at the intersection of the upper row and the column furthest to the right. The idea behind this position was that pico had to drive forward and to the right, making the upper right corner the seemingly ideal choice. However, testing and careful re-evaluation of this position made us realize that pico would give a corridor to the right equal priority to one straight ahead. Therefore, we moved the target point further down the right column. While pico gave right corridors priority over straight corridors, 2 adjacent right corridors with a thin wall in between would result in pico entering the 2nd corridor. To solve this problem, we had to move the target point further down. Once we realized that our artificial blindspots preveted pico from ever going back in previous corridors, we opted to place the target point below pico's possition in the grid, at 30% of the grid height above the lowest row. This target point prioritizes the first corridor to the right, and is even capable of driving circles around a pole. While the latter of those has no practical value, the right hand rule dictates said behavior. It is important to note that, with different parameters in the pathing algorithm and/or artificial blindspots, a target point below pico's position is very dangerous. It can cause pico to turn around randomly, or to spin around his own axis, and should therefore never be implemented without the guarantee that the pathing algorithm and artificial blindspots are properly implemented.
Deadlock
Ever since we implemented Dijkstra's algorithm, we had to take 'deadlocks' into account. In our script, a deadlock is defined as a situation in which the target point cannot be reached. This usually occurs in a dead end, or when the target point is placed inside a wall. With the boundaries implemented in our grid, the latter is impossible. Dead ends, however, do occur regularly in mazes. When we first implemented deadlock detection, pico would sometimes turn around unnecessarily. Whether this was caused by ghost point or the wall memory, which was still implemented at that time, is unknown, but it prompted us to implement a double check for deadlock situations. The deadlock is only recognized if it occurs at least 2 consecutive iterations. After implementing this feature, false deadlocks occurred less frequent, but did not disappear entirely. The few remaining false deadlocks were caused by our second deadlock recognition system. If pico travels significantly less than 0.4m in any time span of 2 seconds, for instance during indecisive behavior, but also when taking sharp corners, a deadlock would be initiated. By re-calibrating the minimum traveled distance threshold, the undesired deadlocks disappeared. After the addition of the artificial blindspots, this second deadlock detection system had become abundant, and was consequently deactivated.
Collision avoidance
When we wrote our collision avoidance algorithm, we wanted to prevent the saw-tooth like behavior displayed by the code used during the corridor competition. In order to achieve this, we wanted to align pico to the closest wall it could find, using a feedback controller. While we did succeed to do so, pico tended to 'stick' to walls, and did not move away from the wall he was following under any circumstance. To prevent this behavior, we removed the 'pull' side of our feedback controller. Now, the collision avoidance only interferes when pico gets to close to a wall. Due to the nature of feedback controllers with a velocity output, pico will end up driving parallel to the wall if the desired drive direction does not change.
HSV thresholds
During the threshold determination for both the red and white color in the arrow detection, microsoft paints color pallet is used. The values for H,S and V here are capped at 239. After implementing these values and testing the script we however observed that OpenCV uses totally different maximum values. Experiments resulted in 180,360 and 360 for H,S and V respectively. Due to a lack of time the HSV values weren't optimized for the final alogithm used in the maze contest. This resulted in the inability to properly read arrows.
Corridor competition
For the corridor competition, our goal was to successfully complete the challenge. Since pico was able to solve even the most badly build corridors, we were confident that our script could find the exit. It turned out that pico could indeed solve the corridor, although in a sub-optimal way. The straight part of the corridor went quite flawless, but taking the turn did not. Since pico stood still while turning, we lost valuable time. Furthermore, due to pico's distance to the wall at that time, the corridor was detected too early. This meant that the collision avoidance had to guide pico through the exit, resulting in a curved path. Nevertheless, our goal to complete the challenge was reached.
Evaluation
We learnt several crucial lessons during the corridor competition. The maze was build properly and straight, which meant that we invested too much in robustness, and too little in performance. Furthermore, our simple approach turned out to be inferior to several other groups, not entirely unexpected. To win, or at least perform above average, at the final maze competition, we would have to design a script that allows smooth movements without unnecessary stops. However, pico did complete the corridor challenge as expected, meaning that we could refine and expand our script, and did not have to start over from scratch.
Final maze competition
First attempt
We had multiple versions of our script ready for the competition. The versions varied from the most basic navigation script, without entrance and exit detection, victory dance and arrow recognition, to the version with all features enabled. The maze of the competition turned out to be relatively simple, but well designed to test each feature required for optimal driving. Therefore, we knew we would not win without the arrow detection, which was not tested in real life yet, and had questionable robustness during simulations. Because we had, and still have, full confidence in the navigational algorithm itself, we opted to run our first try with arrow detection enabled. While it seemed to work momentarily, the script lost track of the first arrow, prompting pico to take the wrong turn. At the end of the corridor, pico correctly detected the deadlock, and started turning. However, during the turn, an unidentified object, most likely the red door, was detected as an arrow. This put the target point at the left side, changing the deadlock turn direction to negative. After turning back a little, the door was out of sight, resetting the turn direction to positive. This process seemed to repeat itself a couple of times, so we elected to abort this attempt.
Second attempt
During the second attempt, we opted to run the script in its most basic version, since entrance detection was not needed. Furthermore, our victory dance could not be performed either, since there was no room available and pico would be turned of once he would cross the finish line. Since we had no arrow detection this time, pico turned to the wrong direction at the first arrow. Once the dead end was in his vision range, pico turned successfully and finished the maze without any further mistakes. The trust in our core navigation turned out to be justified. The end time was 1 minute and 23 seconds, resulting in a respectable fifth position.
Evaluation
The maze challenge went more or less as expected. We had serious doubts about the robustness of the arrow detection, and without proper color thresholds implemented, it would be questionable whether or not pico could even read the arrow. It turned out to be the worst of both cases. Pico could not read the arrow, but another object, most likely the door, was detected as an arrow a few moments later. The lackluster performance of the arrow detection was partially compensated by the effectiveness of our navigator. The high level navigation, calculated with Dijkstra's algorithm, immediately detected aevery dead end, and always sent pico to the corridor deemed optimal by the selected maze solving strategy. The simple, yet effective low level navigation kept pico around the middle of the corridor, and led the robot around corners in a smooth, curved manner. With the exclusion of the dead end turn, pico never stood still, always moving at maximum velocity. The excellent performance of our navigator enabled us to take the 5th spot, above multiple groups with successfull arrow detection.