Embedded Motion Control 2012 Group 11: Difference between revisions
| Line 29: | Line 29: | ||
==Data acquisition and simplification== | ==Data acquisition and simplification== | ||
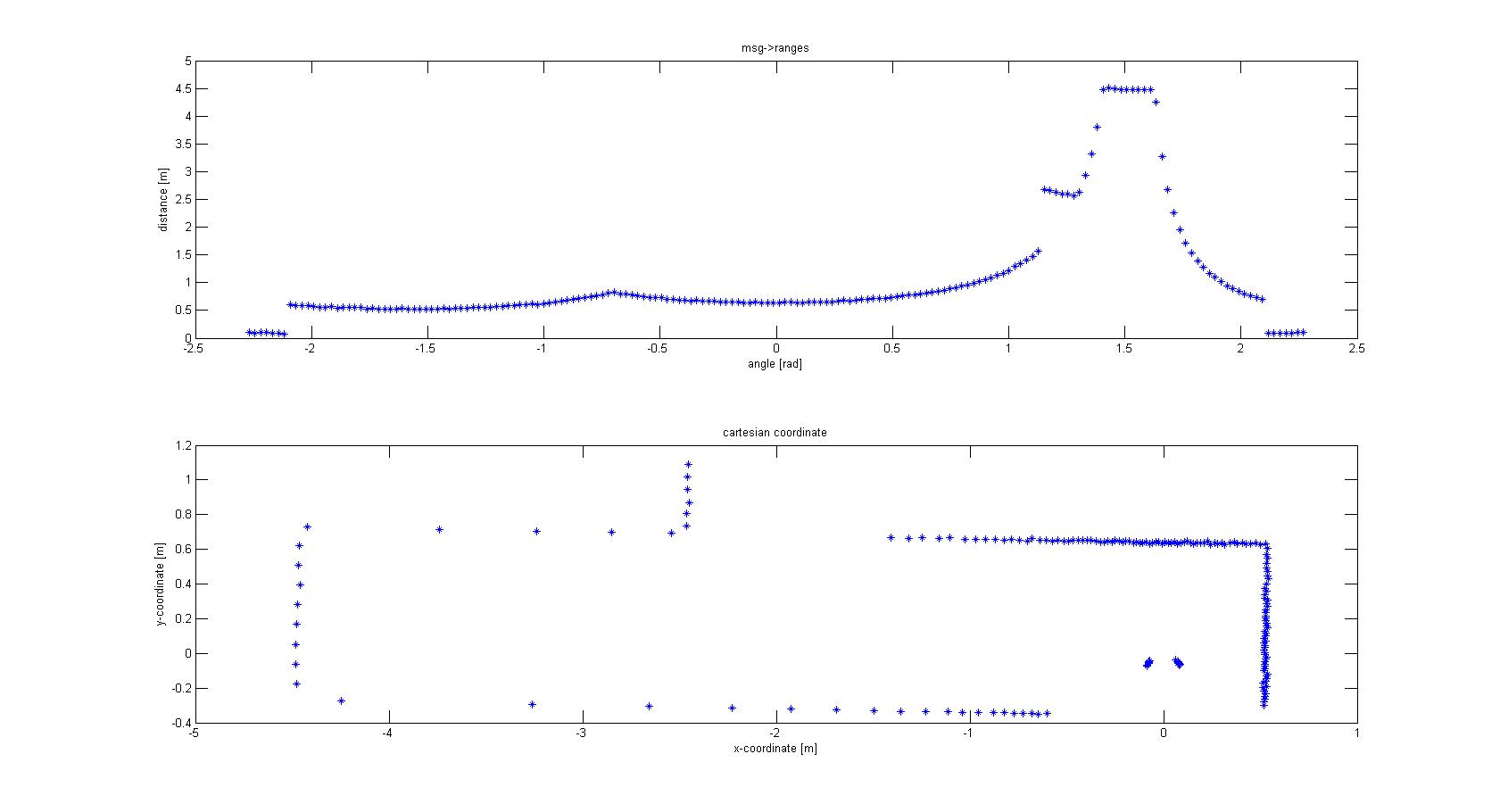
The laser-output from the robot is given in polar coordinates. The first thing done was to make a conversion to Cartesian coordinates to get a better feeling of how to treat the data, and the possibilities this would give for simplification of the data. For this conversion the following data was used: | The laser-output from the robot is given in polar coordinates. The first thing done was to make a conversion to Cartesian coordinates to get a better feeling of how to treat the data, and the possibilities this would give for simplification of the data. For this conversion the following data was used: | ||
* msg->ranges.size() | |||
* msg->angle_min | |||
* msg->angle_max | |||
* msg->ranges[x]; x < ranges->size() | |||
* msg->angle_increment | |||
With basic algebra the conversion was made, which is shown in Figure 1. | With basic algebra the conversion was made, which is shown in Figure 1. | ||
Revision as of 00:01, 15 June 2012
Group Info
| Group Members | Student nr. | |
| Christiaan Gootzen | c.f.t.m.gootzen@student.tue.nl | 0655133 |
| Sander van Zundert | a.w.v.zundert@student.tue.nl | 0650545 |
Tutor
Sjoerd van den Dries - s.v.d.dries@tue.nl
Due to major personnel changes the project was reset in week 7, and a brand new start was made. The results from this point on are reported in the section below.
The project was split into two parts. The first part consists of the basic robot control algorithm. This includes the mapping of the laser data in combination with odometry. With this alignment functions and wall avoidance can be implemented, as well as recognition of corners and junctions. The recognition of a junction marks the jump to the second part of the algorithm: solving the maze. For the corridor competition it is enough to find the first exit and leave the corridor: in the maze the decision making will start at the detection of the junction. The basic robot control algorithm consists of three separate points: data acquisition and simplification of the data, detection of the environment and the response of the robot to the environment.
Data acquisition and simplification
The laser-output from the robot is given in polar coordinates. The first thing done was to make a conversion to Cartesian coordinates to get a better feeling of how to treat the data, and the possibilities this would give for simplification of the data. For this conversion the following data was used:
- msg->ranges.size()
- msg->angle_min
- msg->angle_max
- msg->ranges[x]; x < ranges->size()
- msg->angle_increment
With basic algebra the conversion was made, which is shown in Figure 1.
From the Cartesian plot some decisions can already be made. For instance, the data points that are plotted near the robot will have to be removed, since these are laser points that are projected on the robot itself. Furthermore we see a lot of points that are far away from the robot, all at a distance close to 10 meter. This is the maximum range of the laser points on the simulated robot, but on the real robot this might be different and can give a disturbing input. Therefore the data points which are relevant to the robot is limited to a range of TOO_FAR_TO_MAP meters, which is a static float to be fine-tuned to achieve good vision for the robot without large disturbances or processing time (limiting the data points you take into consideration when making decisions can speed up calculation times).
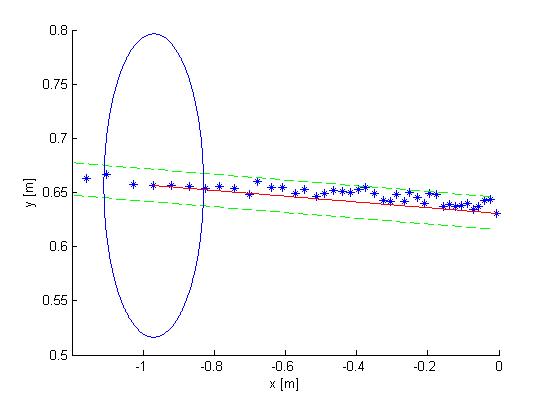
The next observation made from the Cartesian plot was that the data from the laser is actually quite noisy, as can be seen in Figure 2. The points do not align in a nice way, which can complicate decision making and mapping. One option is to make a fit over all the data points using basic functions for the walls instead of the points. This is also shown in Figure 2. If you assume that all the walls are straight (at least the walls are not substantially curved) you can use linear functions to represent the walls. If you do this in a correct manner you will only have to compare the robot position and orientation to the linear functions (i.e. only a zero order and first order constant a0 and a1) of these walls. Since you map only walls that are close to the robot this will reduce the input of your algorithms for wall avoidance from the number of laser points (over one thousand for the real life robot) to the first order functions of the walls (which will generally not exceed 8 wall segments, so 16 constants in total). A good motivation to continue developing an algorithm to do this.
Mapping Algorithm